Цифровые устройства комбинационного типа.

<2 3 456 7 8 >

Дешифратор. Полный двоичный дешифратор, или декодер – это цифровое устройство, преобразующее n-разрядный двоичный позиционный код в сигнал на одном из m=2ⁿ выходов. Таким образом полный двоичный дешифратор имеет n входов и m выходов. Каждому значению входного кода соответствует появление единичного выходного сигнала только на одном из m выходов, при нулях на остальных (m-1) выходах (или наоборот, если дешифратор имеет не прямые, а инверсные выходы).

Логика работы полного двухразрядного двоичного дешифратора с прямыми выходами описывается таблицей истинности (табл. 14.11).

Таблица 14.11

Х₁	Х₀	Y₃	Y₂	Y₁	Y₀

Такой дешифратор имеет n=2 входа Х₁ и Х₀, и m=2²=4 выхода Y₃,Y₂,Y₁ и Y₀. В соответствии с таблицей истинности (табл. 14.11) составим систему логических уравнений, описывающих работу этого дешифратора.

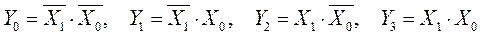
Из полученной системы логических уравнений следует, что для построения такого дешифратора потребуются два элемента НЕ (инвертора), и четыре двухвходовых элемента И. Схема полного двоичного дешифратора на два входа приведена на рис. 14.16а.

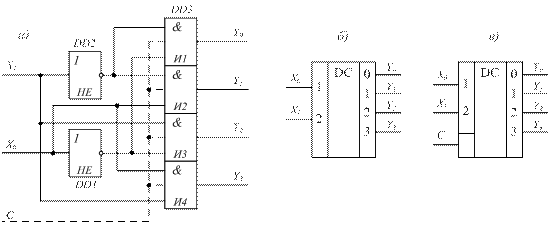
Рис. 14.16. Схема полного двоичного дешифратора на два входа.

Задавая различные комбинации логических уровней сигналов на входах Х₁ и Х₀ в соответствии с таблицей истинности (табл. 14.11), и анализируя состояния уровней сигналов на входах выходных элементов И убедитесь, что единичный логический уровень на каждом выходе появляется только при определенной комбинации входных сигналов.

Если в схеме дешифратора на рис. 14.16а добавить вход синхронизации С (показан пунктиром), то получим синхронизируемый дешифратор. Для этого в данной схеме необходимо использовать элементы И с тремя входами, а система логических уравнений примет вид:

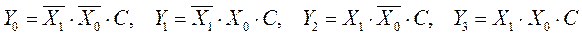
На рис. 14.16б приведено условное графическое обозначение несинхронизируемого двоичного дешифратора на два входа, а на рис. 14.16в – обозначение синхронизируемого двоичного дешифратора тоже на два входа.

Аналогично могут быть построены дешифраторы на любое количество разрядов входного кода. Промышленностью выпускаются готовые микросхемы дешифраторов на два, три и четыре разряда входного кода. Для построения многоразрядных дешифраторов применяют каскадное включение микросхем дешифраторов меньшей разрядности.

Дешифраторы применяются в устройствах управления для дешифрации операций или команд с целью формирования управляющих сигналов.

Демультиплексор. Демультиплексор – это цифровое устройство, выполняющее операцию передачи сигнала с одного информационного входа на любой один из нескольких выходов. Таким образом, демультиплексор имеет один информационный вход Х, k адресных входов (k-разрядный двоичный код а_k_-1, ….a₀), и m=2^k выходов.

Система логических уравнений, описывающая работу демультиплексора, имеет вид:

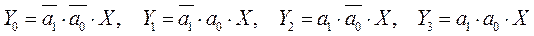
Эта система логических уравнений полностью совпадает с системой логических уравнений синхронизируемого дешифратора. Поэтому такой дешифратор может выполнять функции демультиплексора если синхровход С использовать как информационный (С=Х), входы дешифратора Х₁ и Х₀ использовать как адресные входы демультиплексора, а выходы дешифратора будут выходами демультиплексора.

С помощью демультиплексора возможно распределение информации с одного входа по нескольким различным адресам и преобразование информации из последовательной формы в параллельную.

Шифратор. Шифратор или кодер – это цифровое устройство, выполняющее функцию, обратную дешифратору, то есть преобразует (кодирует) сигнал с одного из входов в двоичный позиционный код. Он имеет (m-1) входов и n выходов (m=2ⁿ). При подаче сигнала на один из входов (только на один) на выходе появляется двоичный код, соответствующий этому входу.

Логика работы двоичного шифратора с n=2 (двухразрядный выходной код) и прямыми выходами описывается таблицей истинности (табл. 14.12).

Таблица 14.12

Х₃	Х₂	Х₁	Х₀	Y₁	Y₀

По табл. 14.12 составим систему логических уравнений, описывающих работу двоичного шифратора:

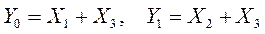
Из полученной системы логических уравнений видно, что для построения такого шифратора потребуются только два элемента ИЛИ (рис. 14.17а).

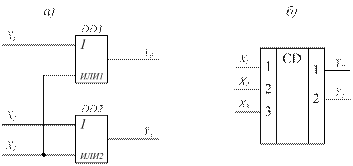
Рис. 14.17. Схема двоичного шифратора с n=2.

Задавая различные комбинации логических уровней сигналов на входах Х₁, Х₂ и Х₃ в соответствии с таблицей истинности (табл. 14.12), и анализируя состояния уровней сигналов на выходах выходных элементов ИЛИ убедитесь, что каждая кодовая комбинация на выходах Y₁ и Y₀ появляется только при поступлении единичного логического сигнала на соответствующий вход Х_i. При этом вход Х₀ отсутствует, так как комбинация входных сигналов Х₁=Х₂=Х₃=0 эквивалентна Х₀=1. Поэтому число входов шифратора на один меньше, чем число наборов выходного кода.

На рис. 14.17б приведено условное графическое обозначение (для функциональных схем) полного двоичного шифратора для n=2.

Аналогично могут быть построены двоичные шифраторы для любой разрядности выходного кода.

Мультиплексор. Мультиплексор – это цифровое устройство, выполняющее операцию передачи сигнала с любого информационного входа на один выход. Мультиплексор выполняет функцию, обратную функции демультиплексора.

Мультиплексор имеет k адресных входов (а_k_-1, …. а₀), имеет n=2^k информационных входов (Х_n_-1, … Х₀) и один выход Y. С выходом Y соединяется тот вход Х_i, адрес которого определяется кодом адресных входов (а_k_-1, …. а₀).

Логика работы мультиплексора на четыре информационных входа (n=4) с двумя адресными входами (k=2, так как n=2^k=4) описывается таблицей истинности (табл. 14.13).

Таблица 14.13

a₁	a₀	Y
		X₀ X₁ X₂ X₃

По табл. 14.13 составим алгебрологическое уравнение, описывающее работу такого мультиплексора:

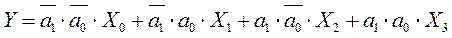
Из полученного логического уравнения видно, что для построения такого мультиплексора потребуются два элемента НЕ, четыре трехвходовых элемента И и один элемент ИЛИ на четыре входа (рис. 14.18а).

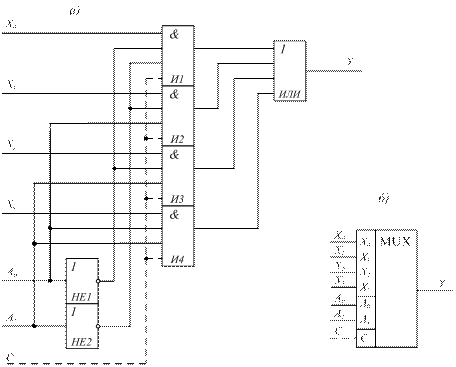
Рис. 14.18. Схема мультиплексора на четыре информационных входа.

При анализе работы схемы, задавая различные кодовые комбинации на адресные входы убедитесь в справедливости табл. 14.13. Аналогично могут быть построены мультиплексоры на большее количество информационных входов.

На рис. 14.18б приведено условное графическое обозначение (для функциональных схем) мультиплексора с n=4 и k=2.

Мультиплексоры бывают синхронизируемые и несинхронизируемые. В синхронизируемых мультиплексорах добавляется вход синхронизацмм С (показан пунктиром на рис. 14.18а).

Мультиплексоры применяются для переключения магистралей (шин) передачи цифровой информации. Готовые мультиплексоры выпускаются в виде интегральных микросхем до n=8.

Схема сравнения. Схема сравнения (компаратор) – это цифровое устройство, выполняющее операцию сравнения двух чисел А и В. Результатом сравнения является обнаружение состояний А=В, А>В или А<В.

Схемы сравнения бывают одноразрядные и многоразрядные. Одноразрядная схема сравнения имеет два входа, соответственно вход числа А (один бит) и вход числа В (один бит), и три выхода, соответственно Y_A₌_B, Y_A_>_B и Y_A_<_B. Логика работы одноразрядной схемы сравнения описывается таблицей истинности (табл. 14.14).

Таблица 14.14

A	B	Y_A>B	Y_A=B	Y_A<B

По табл. 14.14 составим систему логических уравнений, описывающих работу одноразрядной схемы сравнения:

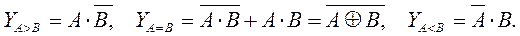
Из полученной системы логических уравнений видно, что для построения такой схемы сравнения потребуются три элемента НЕ, два элемента И и один элемент ИСКЛЮЧАЮЩЕЕ ИЛИ (рис. 14.19).

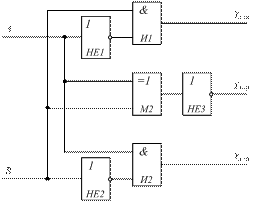
Рис. 14.19. Реализация схемы сравнения (компаратора).

При анализе работы схемы 14.19, задавая различные кодовые комбинации на входы А и В убедитесь в справедливости табл. 14.14.

Многоразрядные схемы сравнения сравнивают числа начиная со старших разрядов. На выход такой схемы сравнения передается результат сравнения самых старших из несовпадающих разрядов. Естественно, многоразрядные схемы сравнения гораздо сложнее.

Двоичный сумматор. Сумматор - это цифровое устройство, выполняющее операцию сложения двоичных чисел. При сложении двух одноразрядых чисел А и В возможны следующие комбинации:

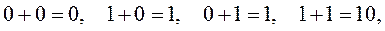
где «+» - арифметическое сложение.

При А=В=1 происходит перенос в старший разряд. Поэтому одноразрядный двоичный сумматор имеет два входа А₀ и В₀, и два выхода – выход суммы S₀, и выход переноса в старший разряд С₁. Логика работы одноразрядного двоичного сумматора описывается таблицей истинности (табл. 14.15).

Таблица 14.15

A₀	B₀	S₀_>B	C₁

По табл. 14.15 составим систему логических уравнений, описывающих работу одноразрядного двоичного сумматора:

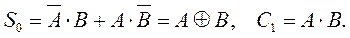
Из полученной системы логических уравнений видно, что для построения одноразрядного двоичного сумматора потребуются один элемент ИСКЛЮЧАЮЩЕЕ ИЛИ и один элемент И (рис. 14.20а).

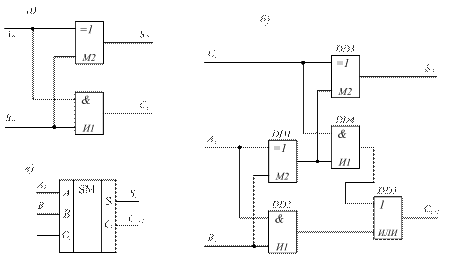
Рис. 14.20. Схемы одноразрядных сумматоров.

При анализе работы схемы 14.20а, задавая различные кодовые комбинации на входы А₀ и В₀ убедитесь в справедливости табл. 14.15. Такой одноразрядный двоичный сумматор с двумя входами называется полусумматором (ПСМ).

При сложении двух многоразрядных двоичных чисел полусумматор можно использовать только для младшего разряда. Это связано с тем, что в более старших разрядах складываются не два, а три бита, с учетом переноса из младшего разряда. Такой одноразрядный двоичный сумматор с тремя входами называется полный одноразрядный сумматор (ПОС). Его строят с использованием двух полусумматоров (рис. 14.20б).

Один полусумматор на элементах D1 и D2 суммирует два бита А_i и В_i, второй полусумматор на элементах D3 и D4 суммирует выход суммы первого полусумматора с битом переноса из младшего разряда С_i и выдает результат суммы S_i, а элемент D5 (элемент ИЛИ) формирует перенос в старший разряд С_i₊₁.