Логические основы цифровых устройств.
Для формального описания узлов цифровых устройств при их анализе и синтезе используется аппарат алгебры логики (булевой алгебры).
В алгебре логики различают двоичные переменные (аргументы) и логические (переключательные) функции. Двоичные переменные могут принимать только два значения: 0 и 1, и обозначаются символами х1, х2, х3 и т.д. Логические функции как и аргументы могут принимать лишь два значения: 0 или 1, и обозначаются как функции f(x1, x2,…), либо в виде y1, y2,… .
Логические функции могут быть заданы либо в виде алгебрологических выражений, включающих операторы и операнды, либо в виде таблиц истинности, в которых для всех наборов аргументов указываются значения логических функций. Число наборов аргументов в таблице истинности ограничено числом 2n, где n-количество аргументов.
Любая логическая функция может быть выражена в виде комбинации элементарных логических функций. К элементарным логическим функциям относятся всего три функций, это функции «И», «ИЛИ», «НЕ».
Техническая реализация логических функций осуществляется логическими элементами (электронными схемами), которые называются также, как и реализуемые логические функции. На физическом уровне логические сигналы 1 и 0 представляются в виде уровней напряжений (рис. 14.1а). Условные графические обозначения логических элементов «И», «ИЛИ», «НЕ» приведены на рис. 14.1б.

Рис. 14.1. Физическое представление логических сигналов и условные
графические обозначения логических элементов
Сигнал логической 1 представляется обычно уровнем напряжения примерно U1=5, 9, или 15В, в зависимости от серии используемых микросхем. Сигнал логического 0 представляется обычно отсутствием напряжения U0 около 0,4В.
Логическая функция «И» (конъюнкция, логическое умножение) может иметь два и более аргументов. При этом функция принимает значение 1, если все аргументы одновременно равны 1,и функция принимает значение 0, если хотя бы один из аргументов равен 0. Отсюда и название функции «И», так как она принимает значение 1, только если и первый, и второй , и все остальные аргументы равны 1.
Аналитическая форма представления конъюнкции (функции И) от двух переменных Х1 и Х2 имеет вид: f1(Х1,Х2)= Х1ּХ2 или f1(Х1,Х2)= Х1&Х2.
Табличная форма представления (таблица истинности) конъюнкции (функции И) от двух переменных Х1 и Х2 имеет вид (табл. 14.2):
Таблица 14.2.
| Х1 | Х2 | f1 |
Условное обозначение логического элемента, реализующего логическую функцию И от двух аргументов, приведено на рис. 14.1б.
Логическая функция «ИЛИ» (дизъюнкция, логическое сложение) может иметь два и более аргументов. При этом функция принимает значение 0, если все аргументы одновременно равны 0,и функция принимает значение 1, если хотя бы один из аргументов равен 1. Отсюда и название функции «ИЛИ», так как она принимает значение 1, если или первый, или второй , или все остальные аргументы равны 1.
Аналитическая форма представления дизъюнкции (функции ИЛИ) от двух переменных Х1 и Х2 имеет вид: f2(Х1,Х2)= Х1+Х2 или f2(Х1,Х2)= Х1VХ2.
Табличная форма представления (таблица истинности) дизъюнкции (функции ИЛИ) от двух переменных Х1 и Х2 имеет вид (табл. 14.3):
Таблица 14.3.
| Х1 | Х2 | f2 |
Условное обозначение логического элемента, реализующего логическую функцию ИЛИ от двух аргументов, приведено на рис. 14.1б.
Логическая функция «НЕ» (отрицание) может иметь только один аргумент. При этом функция принимает значение 1, если аргумент равен 0,и функция принимает значение 0, если аргумент равен 1. Отсюда и название функции «НЕ», так как она принимает значения противоположные значению аргумента.
Аналитическая форма представления отрицания (функции НЕ) имеет вид: f3(Х)= 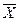
Табличная форма представления (таблица истинности) отрицания (функции НЕ) имеет вид (табл. 14.4):
Таблица 14.4.
| Х | f3 |
Условное обозначение логического элемента, реализующего логическую функцию НЕ, приведено на рис. 14.1б.
Широкое применение на практике находят более сложные (комбинированные) логические элементы, реализующие более сложные логические функции, и выпускаемые в виде интегральных микросхем.
Отрицание конъюнкции (логическая функция И-НЕ). Эта функция образуется путем отрицания результата, получаемого при выполнении операции И.
Аналитическое представление функции И-НЕ от двух аргументов:
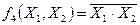 .
.
Табличная форма представления (таблица истинности) функции И-НЕ) от двух переменных Х1 и Х2 имеет вид (табл. 14.5):
Таблица 14.5.
| Х1 | Х2 | f4 |
Такая логическая функция может быть реализована при последовательном соединении логического элемента И с двумя входами, и логического элемента НЕ. Условное обозначение логического элемента И-НЕ приведено на рис 14.2а.
Отрицание дизъюнкции (логическая функция ИЛИ-НЕ). Эта функция образуется путем отрицания результата, получаемого при выполнении операции ИЛИ.
Аналитическое представление функции ИЛИ-НЕ от двух аргументов:
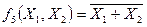 .
.
Табличная форма представления (таблица истинности) функции ИЛИ-НЕ) от двух переменных Х1 и Х2 приведена в табл. 14.6.
Такая логическая функция может быть реализована при последовательном соединении логического элемента ИЛИ с двумя входами, и логического элемента НЕ. Условное обозначение логического элемента ИЛИ-НЕ приведено на рис 14.2б.
Таблица 14.6.
| Х1 | Х2 | f5 |
ИСКЛЮЧАЮЩЕЕ ИЛИ (операция НЕРАВНОЗНАЧНОСТЬ или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА). Обычно эта логическая функция от двух аргументов. Эта функция принимает значение 1, если значения аргументов Х1 и Х2 противоположны.
Аналитическое представление функции ИСКЛЮЧАЮЩЕЕ ИЛИ от двух аргументов:
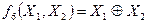 .
.
Табличная форма представления (таблица истинности) функции ИСКЛЮЧАЮЩЕЕ ИЛИ) от двух переменных Х1 и Х2 имеет вид (табл. 14.7):
Таблица 14.7.
| Х1 | Х2 | F6 |
Такая логическая функция может быть реализована с помощью функций И, ИЛИ,НЕ в соответствии с логическим выражением:
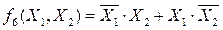
Для реализации такой логической функции потребуются два элемента НЕ, два элемента И и один элемент ИЛИ. В наборах выпускаемых интегральных микросхем выпускаются элементы ИСКЛЮЧАЮЩЕЕ ИЛИ, реализующие указанную функцию. Условное обозначение логического элемента ИЛИ-НЕ приведено на рис 14.2в.
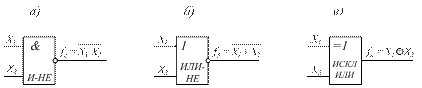
Рис. 14.2. Условные графические обозначения логических элементов.
Законы алгебры логики. В алгебре логики используются четыре основных закона: переместительный, сочетательный, распределительный и закон инверсии. Эти законы позволяют проводить эквивалентные преобразования логических функций, выраженных с помощью функций И, ИЛИ, НЕ, упрощать и минимизировать их.
Переместительный закон аналогичен переместительному закону обычной алгебры и записывается в виде:
а) для дизъюнкции 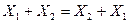 ;
;
б) для  конъюнкции
конъюнкции 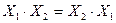 .
.
Таким образом, от перемены мест слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.
Сочетательный закон также аналогичен сочетательному закону обычной алгебры и записывается в виде:
а) для дизъюнкции 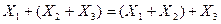 ;
;
б) для  конъюнкции
конъюнкции 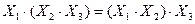 .
.
Следовательно, можно группировать переменные, объединенные знаком дизъюнкции или конъюнкции, это не меняет значений логических функций.
Распределительный закон аналога в обычной алгебре не имеет, и записывается в виде:
а) для дизъюнкции 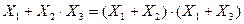 ;
;
б) для  конъюнкции
конъюнкции 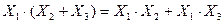 .
.
Справедливость распределительного закона доказывается путем составления таблиц истинности для левой и правой частей каждого выражения..
Закон инверсии:
а) для дизъюнкции 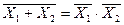 ;
;
б) для  конъюнкции
конъюнкции 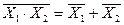 .
.
Справедливость закона инверсии также доказывается путем составления таблиц истинности для левой и правой частей каждого выражения..
Контрольные вопросы
1. Понятие логических функций, способы их задания и применение)?
2. Элементарные логические функции, их алгебро-логические выражения и таблицы истинности?
3. Логические функции И-НЕ и ИЛИ-НЕ, формы их представления?
4. Логическая функция ИСКЛЮЧАЮЩЕЕ ИЛИ (Сумма по Мод2), формы ее представления?
5. Основные законы алгебры логики?
6. Выражения переместительного закона для конъюнкции и дизъюнкции?
7. Выражения сочетательного закона для конъюнкции и дизъюнкции?
8. Выражения распределительного закона для конъюнкции и дизъюнкции?
9. Выражения законов инверсии для конъюнкции и дизъюнкции?
10. Условные графические обозначения логических элементов?
11. Физическая форма представления логических сигналов?
Дата добавления: 2020-10-14; просмотров: 1057;











