Применение теоремы Гаусса
Поле равномерно заряженной плоскости
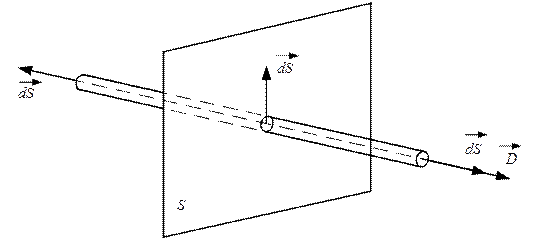
Плоскость бесконечно большая. Поле равномерно, следовательно, вектор 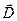 имеет такое же направление, что и вектор нормали
имеет такое же направление, что и вектор нормали 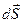 заряженной плоскости. Построим вокруг плоскости цилиндрическую поверхность, состоящую из боковой и двух торцевых поверхностей. Поток вектора электрического смещения
заряженной плоскости. Построим вокруг плоскости цилиндрическую поверхность, состоящую из боковой и двух торцевых поверхностей. Поток вектора электрического смещения 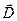 перпендикулярен нормали боковой поверхности цилиндра. Поэтому скалярное произведение
перпендикулярен нормали боковой поверхности цилиндра. Поэтому скалярное произведение 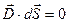 и поток вектора электрического смещения
и поток вектора электрического смещения 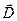 через боковую поверхность цилиндра равен нулю. Поток будет пронизывать только две торцевые поверхности. Причем вектор нормали торцевой поверхности направлен также как и вектор электрического смещения
через боковую поверхность цилиндра равен нулю. Поток будет пронизывать только две торцевые поверхности. Причем вектор нормали торцевой поверхности направлен также как и вектор электрического смещения 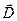 . Тогда по теореме Гаусса:
. Тогда по теореме Гаусса:

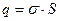 ,
,
где  – поверхностная плотность заряда.
– поверхностная плотность заряда.
Электрическое смещение постоянно, вынесем его за знак интеграла:
 .
.
Так как торцевых поверхностей две, то:
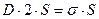
 .
.
А так как
 ,
,
то напряженность равна:

Электрическое смещение, как и напряженность, во всех точках пространства одинаково, так как поле равномерно.
Поле двух параллельно расположенных плоскостей имеющих разные заряды +Q и -Q

Поле будет существовать только между пластинами, вне их поля нет.
Напряженность поля между пластинами:
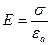

Рассмотрим плоский конденсатор. Если обкладки плоского конденсатора не бесконечно большие, то на краях обкладок имеются места выпучивания силовых линий. Это явление называют краевым эффектом. Электростатическое поле на краях обкладок не равномерно и вычислить его сложно. Поэтому, если поверхность электродов гораздо больше, чем расстояние между ними, то краевым эффектом пренебрегают и считают поле равномерным.
Поле равномерно заряженного шара

Заряд q равномерно распределен в шаровой области радиуса А. Проведем сферическую поверхность S радиусом R, начало системы координат которой находится в центре шаровой области. Диэлектрическая проницаемость шаровой области равна  , а внешней среды
, а внешней среды  .
.
1. Рассмотрим случай, когда R>A – исследуемая точка находиться вне шаровой области. Задача обладает шаровой симметрией, то есть для всех точек, равноудаленных от начала координат, модуль вектора напряженности электростатического поля будет иметь одно и тоже значение.
По теореме Гаусса:

Вектор напряженности электростатического поля 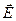 и вектор нормали
и вектор нормали 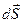 направлены в одну сторону. Поэтому
направлены в одну сторону. Поэтому  . Так как напряженность постоянна, ее можно вынести из за знака интеграла.
. Так как напряженность постоянна, ее можно вынести из за знака интеграла.

Площадь сферы равна 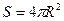 , тогда:
, тогда:
 ,
,
где  .
.

Полученная формула совпадает с формулой напряженности точечного заряда помещенного в центр шара, тогда формула потенциала будет иметь следующий вид (вывод смотри в теме потенциал электростатического поля):

2. Рассмотрим случай, когда R<A – исследуемая точка находиться внутри шаровой области.
Левая часть теоремы Гаусса преобразуется точно также:
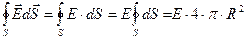 .
.
Правая часть уравнения изменится, так как внутри выделенного объема находится не весь заряд q, а только его часть.
 – объемная плотность заряда;
– объемная плотность заряда;
 ,
,
где объем шара:
 .
.
Полный заряд внутри шаровой области радиуса А:
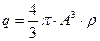 .
.
Заряд внутри выделенного объема радиуса R:
 .
.
Частичный заряд внутри выделенного объема:
 .
.
Напряженность поля, когда исследуемая точка находиться внутри шаровой области:
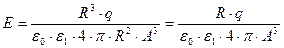 .
.

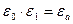 ;
;
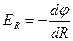 ;
;
 .
.
Построим графики зависимости напряженности, электрического смещения и потенциала от радиуса.

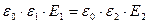 .
.
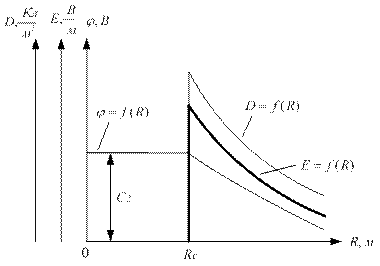
Электрическое смещение не зависит от свойств среды, поэтому, на границе раздела двух сред, скачков модуля электрического смещения не бывает. Напряженность электростатического поля, наоборот, зависит от свойств среды, поэтому на границе раздела двух сред меняется скачком. График зависимости потенциала от расстояния зависит от того, где потенциал был принят равным нулю. Пусть в нашем случае точка с нулевым потенциалом лежит в бесконечности. График потенциала – это плавно изменяющаяся функция, так как потенциал – это работа по перемещению заряда.
Поле равномерно заряженной сферы

Заряд равномерно распределен по поверхности сферы.
 – поверхностная плотность заряда
– поверхностная плотность заряда
 ;
;
 .
.
При рассмотрении поля вне сферы рассуждения такие же, что и для шара
при R > А (Rс):

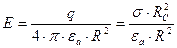 ;
;
 .
.
При R < Rс заряда нет, так как он равномерно распределен по поверхности сферы
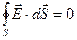
Поле отсутствует, Е=0.
Потенциал равен постоянной интегрирования,  .
.
Построим графики зависимости напряженности, электрического смещения и потенциала от радиуса.
Поле равномерно заряженной оси
(бесконечно тонкого провода)


На заряженной оси заряд Q равномерно распределен по длине.
Вокруг оси построим цилиндрическую поверхность произвольного радиуса r.
Применим теорему Гаусса:
 ;
;
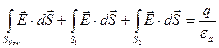
На торцевой поверхности вектора 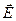 и
и 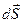 перпендикулярны, следовательно, поток через них равен 0 (весь поток идет через боковую поверхность). Напряженность поля постоянна, следовательно, ее можно вынести за знак интеграла.
перпендикулярны, следовательно, поток через них равен 0 (весь поток идет через боковую поверхность). Напряженность поля постоянна, следовательно, ее можно вынести за знак интеграла.
 ,
,  ;
;
 ;
;
 ,
, 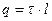 ;
;
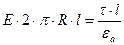 ;
;
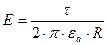 .
.
Найдем потенциал:

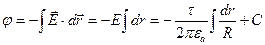 ;
;
 .
.
Для нахождения постоянной интегрирования примем, что точка нулевого потенциала лежит на расстоянии R=R0.
 ;
;
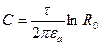 ;
;
 ,
,
где R – расстояние от провода до исследуемой точки,
R0 – расстояние от провода до точки с нулевым потенциалом.
Если радиус бесконечно тонкого провода не стремится к 0, то внутри провода Е=0 и потенциал постоянен (поле отсутствует). Вне провода поле рассчитывают по тем же формулам.
Если точка с нулевым потенциалом лежит в бесконечности, то С = 0.
Поле двух параллельно заряженных осей
Две параллельно заряженные оси несут одинаковый и противоположный по знаку заряд Q.

Пользуясь методом наложения:
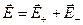 ;
;
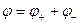 ;
;
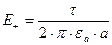 ,
, 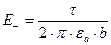 ;
;
 ,
,
где  .
.
Если менять расстояния а и b, так чтобы их отношение оставалось постоянным, получим совокупность точек с одинаковым потенциалом – эквипотенциальную линию.

Потенциал точки 1 выше, так как положение этой точки ближе всех к положительному полюсу, напряженность электростатического поля выше в точке 3, так как это самый маленький квадрат.
Если размеры поперечного сечения сопоставимы с проводом, то в проводах происходит смещение зарядов. Для учета этого смещения вводят понятие электрической оси.

Электрические оси – это такие оси, на которых надо сосредоточить заряды проводов, чтобы поверхности проводов являлись эквипотенциалями. Если на этой оси сосредоточить заряд, картина поля не измениться.
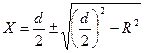 ,
,
где Х – расстояние от геометрической оси до электрической.
Дата добавления: 2020-10-14; просмотров: 563;











