Функция автокорреляции для случайного процесса является аналогом функции размытия линии описывающий детерминированный процесс.
Фурье преобразование функции автокорреляции даёт спектральную плотность мощности шума.
Спектральная плотность мощности шума:
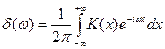
Можем получить некоторую зависимость:
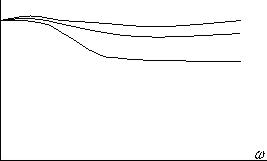
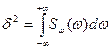
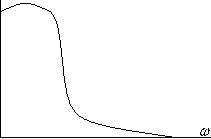
Шум имеющий функцию автокорреляции стремящуюся к 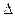 -функции, называемой белым шумом; он имеет равномерный спектр без спада во всём диапазоне пространственных частот.
-функции, называемой белым шумом; он имеет равномерный спектр без спада во всём диапазоне пространственных частот.
Белый шум – обычно невозможен (полностью белый шум) и речь идёт о квазибелом шуме, в котором в некотором пространстве частот близок к белому а в некотором диапозоне идёт спад.
Квазибелый шум – это шум с равномерным не зависящим от частоты распределением спектральной мощности в определённом диапазоне пространственных частот.
Стационарные шумы
Случайный шум называется стационарным, если все его статистические свойства описаны с помощью корреляционных моментов и они инвариантны относительно произвольного начала отсчёта пространства или времени.
Импульсный случайный шум. Методы описания.
Импульсный случайгый шум весьма многообразен. Может меняться всё: момент появления, знак, амплитуда.
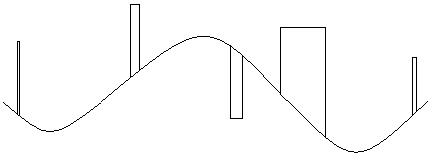
Рассмотрим случай когда шум у нас имеет постоянный знак и имеет два значения:

Случайность заключается в случайной точке пространства, случайная частота, случайная ширина. Но величина их постоянна.
Эти шумы будут характеризоваться шириной амплитуды
Они будут характеризоваться по уровню 0 и 1
Если паузе нужного значения 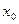 , а средняя длительность импульса при единичном значении амплитуды равна
, а средняя длительность импульса при единичном значении амплитуды равна 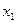 , то вероятность появления амплитудного значения 0 и 1 можно оценить как
, то вероятность появления амплитудного значения 0 и 1 можно оценить как 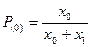 ;
; 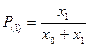 .
.
Сами эти параметры не зависимы друг от друга и распределены по экспоненциальному закону.
Среднее значение ожидания: 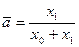
Для автокорреляционной функции талого шума получено выражение
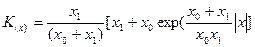
Для спектральной мощности шума это выражение записывается как
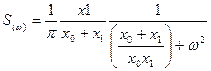
Для импульсного шума
Взаимосвязь сигнала и шума. Понятие об отношении сигнал-шум.
В какой степени зависит величине шума от величины сигнала. Благодаря этому мы выделяем сигнал из шума.
Если статистические характеристики шума не зависят от величины сигнала, то такой шум называется аддитивным .
Общая величина сигнала – будет суммой сигнала и шума
Если статестические характеристики шума зависят от характеристики сигнала, то такой шум называется мультипликативным шумом.
При мультипликативном сигнале величины сигнала от шума перемножается с неким коэффициентом k: 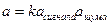
Аддитивный или аддитивно-мультипликативный сигнал:
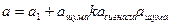
Понятие сигнал-шум
Если мы имеем большую величину шума и большую величину сигнала, то даже при ослаблении сигнала мы можем ослабляя шум, получить хорошее считывание.
Если величины шума и сигнала сопоставимы то в таком случае попытки подавиьь шум приводят к потери информации.
Поэтому во многих случаях сигнал /шум наиболее важным является отношение сигнал/шум
В фотографических системах отношение сигнал-шум принимается как
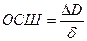
Дата добавления: 2016-07-22; просмотров: 4558;











