Систематические погрешности
Систематическая погрешность q – это составляющая погрешности измерения, которая остаётся постоянной или закономерно изменяется при повторных измерениях.
К систематическим погрешностям измерений можно отнести те составляющие, для которых можно считать доказанным наличие функциональных связей с вызывающими их аргументами. Для них можно предложить следующее определение: систематическая погрешность – закономерно изменяющаяся составляющая погрешности измерений.
Формально это записывается в виде
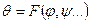 ,
,
где 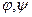 – аргументы, вызывающие систематическую погрешность. Главной особенностьюсистематической погрешности являетсяпринципиальная возможность ее выявления, прогнозирования и однозначной оценки, если удается узнать вид функции и значения аргументов.
– аргументы, вызывающие систематическую погрешность. Главной особенностьюсистематической погрешности являетсяпринципиальная возможность ее выявления, прогнозирования и однозначной оценки, если удается узнать вид функции и значения аргументов.
Одной из основных задач обработки результатов эксперимента является выявление, оценка величины и, по возможности, устранение всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче постоянных. Для выявления постоянной систематической погрешности необходимо выполнить измерения хотя бы двумя различными способами или методами. Обнаруженные и оцененные систематические погрешности исключаются из результатов путем введения поправок.
В зависимости от причин возникновения систематические погрешности подразделяют на следующие виды:
1. Погрешности метода или модели, которые обычно называют методическими погрешностями, например: определение плотности вещества без учета имеющихся в нем примесей, использование формул, не совсем точно описывающих явление, и др.
2. Погрешности воздействия внешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей.
3. Погрешности, возникающие из-за неточности действий или личных качеств оператора (экспериментатора), называемые субъективными погрешностями.
4. Инструментальные (приборные, аппаратурные) погрешности, обусловленные схемными, конструктивными и технологическими несовершенствами средств измерения, их состоянием в процессе эксплуатации. Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов его эксплуатации, неправильное положение прибора и т. п. За исключением смещения начала отсчета, приборные погрешности относятся к разряду неустранимых погрешностей.
В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных факторов, многие из которых невозможно рассчитать, подавить или выявить в данном эксперименте. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученных с помощью серийного (рабочего) и более точного образцового приборов. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности является слишком дорогим. Поэтому на практике различные составляющие систематической погрешности пытаются устранить с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений при условии, что погрешность данного вида по величине и знаку известна. После внесения поправок влияние систематической погрешности данного вида на результат и погрешность измерения устраняется полностью. Если же систематическая погрешность неизвестна, но имеет известные границы изменения, то её учитывают в результате измерения.
В зависимости от характера измерения систематические погрешности подразделяют на элементарные и изменяющиеся по сложному закону.
Элементарные погрешности можно условно разделить на постоянные, прогрессирующие (прогрессивные) и периодические. Прогрессирующими называют монотонно возрастающие или монотонно убывающие погрешности. Периодические погрешности – погрешности, изменение которых можно описать периодической функцией. Погрешности, изменяющиеся по сложному закону, образуются при объединении нескольких систематических погрешностей.
Постоянные систематические погрешности представлены в графической форме на рисунке 3.2 а ( 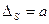 , или
, или 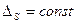 ), а переменные – на рисунке 3.2 б – е. Простейшие переменные систематические погрешности, которые аппроксимируют графиками без перегибов (монотонно изменяющиеся или прогрессирующие) показаны на рисунке 3.2 б – г, а периодические или гармонические погрешности – на рисунке 3.2 е.
), а переменные – на рисунке 3.2 б – е. Простейшие переменные систематические погрешности, которые аппроксимируют графиками без перегибов (монотонно изменяющиеся или прогрессирующие) показаны на рисунке 3.2 б – г, а периодические или гармонические погрешности – на рисунке 3.2 е.
Всем известны "спешащие" и "отстающие" часы, погрешности которых прогрессируют во времени, но мало кто анализирует показания часов за полный оборот стрелки. Если оценивать погрешности, то можно утверждать, что в результате многократного повторения вращения стрелки часов должны проявляться периодические погрешности, обусловленные эксцентриситетом и превращающиеся в нуль при завершении каждого полного оборота.
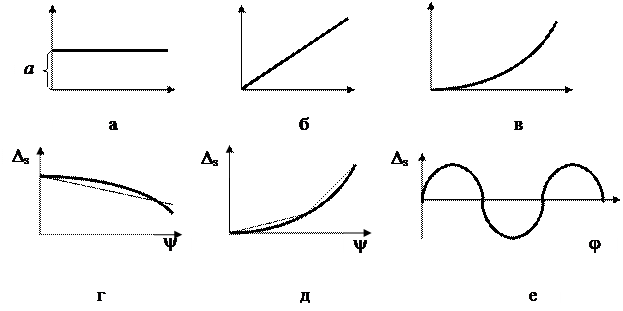 |
Рисунок 3.2 - Виды простейших систематических погрешностей: а – постоянные, б, в – прогрессирующие (линейная и нелинейная), г, д – прогрессирующие нелинейные (предложены варианты аппроксимации прямыми линиями), е – периодические (гармонические).
Обычно для описания и для аппроксимации систематической погрешности подбирают наиболее простую функцию, например линейную для прогрессирующей погрешности. Такой же упрощенный подход применяют и для аппроксимации гармонической систематической погрешности, которая может быть описана как синусоида, косинусоида, пилообразная либо другая периодическая функция.
Систематическая погрешность может иметь не только элементарный, но и более сложный характер, который можно аппроксимировать функцией, включающей приведенные простые составляющие.
Сложная систематическая погрешность, включающая постоянную, прогрессирующую и периодическую составляющую, в общем виде может быть описана выражением
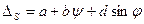 ,
,
где 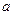 – постоянная составляющая сложной систематической погрешности;
– постоянная составляющая сложной систематической погрешности; 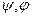 – соответственно аргументы прогрессирующей и периодической составляющих сложной систематической погрешности.
– соответственно аргументы прогрессирующей и периодической составляющих сложной систематической погрешности.
Дата добавления: 2020-10-14; просмотров: 692;











