Постановка задач лінійного програмування, їх моделі та основні форми

Структурні складові економічної системи мають мету (ціль) свого розвитку та функціонування. Це може бути, наприклад, отримання максимуму чистого прибутку, обсягу виробництва, мінімуму витрат чи відходів та інше. Ступінь досягнення мети, в більшості випадків, має кількісну характеристику, тобто її можна описати математично. Нехай Z - обрана ціль.

Загальну лінійну математичну модель формалізації економічних процесів і явищ (загальну задачу лінійного програмування), можна подати у вигляді:

знайти максимум (мінімум) функції

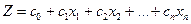(3.1)

за умов

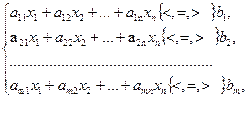(3.2)

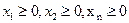(3.3)

Функцію Z називають цільовою функцією або функцією мети. Для економічної системи це є функція ефективності її функціонування та розвитку.

Сформулюємо загальне визначення задачі лінійного програмування таким чином:

Необхідно знайти такі значення керованих змінних х_і, щоб цільова функція при цих значеннях набувала екстремального (мінімального чи максимального) значення за виконання певної множини умов. Отже, потрібно знайти значення змінних 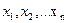, які задовольняють умови (3.2) і (3.3), при яких цільова функція (3.1) набуває екстремального (максимального чи мінімального) значення.

Система (3.2)-(3.3) називається системою обмежень або системою умов задачі. Вона описує внутрішні технологічні та економічні процеси функціонування і розвитку виробничо-економічної системи, а також процеси зовнішнього середовища, які впливають на результат діяльності системи. Для економічних систем змінні х_імають бути невід’ємними. Формалізований запис задачі (3.1)-(3.3) є загальною економіко-математичною моделлю функціонування умовної економічної системи. Розробляючи окреслену модель, потрібно керуватися такими правилами:

1) модель має адекватно описувати реальні економічні та технологічні процеси;

2) у моделі потрібно враховувати все істотне, суттєве в досліджуваному явищі чи процесі, відкидаючи все другорядне, неістотне;

3) модель має бути зрозумілою для користувача;

4) треба забезпечити, щоб множина наборів х_ібула непустою. Для цього в економіко-математичних моделях потрібно якнайменше використовувати обмеження-рівності, а також суперечливі обмеження.

Будь-який набір змінних 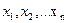що задовольняє умови (3.2) та (3.3), називають допустимим планом або планом. Очевидно, що кожний допустимий план є відповідною стратегією економічної системи, програмою дій. Кожному допустимому плану відповідає значення цільової функції, яке обчислюється за формулою (3.1). Сукупність усіх розв’язків систем обмежень (3.2) та (33), тобто множина всіх допустимих планів, становить область існування планів. План, за якого цільова функція набуває екстремального значення, називається оптимальним. Оптимальний план є розв’язком задачі математичного програмування (3.1)-(3.3).

Відзначимо, що в задачі математичного програмування передбачається одна цільова функція, яка кількісно виражена. В реальних економічних системах на роль критерію оптимальності (ефективності) претендують багато показників. Наприклад, максимум чистого доходу від виготовленої продукції чи максимум рентабельності, мінімум собівартості виготовленої продукції або мінімум витрат дефіцитних ресурсів тощо. Хоча загальна задача математичного програмування передбачає одну цільову функцію, але існують математичні методи побудови компромісних планів, тобто методи багатокритеріальної оптимізації. Розглянемо найпростіші математичні моделі задач лінійного програмування (ЛП):

1) Задача про використання ресурсів (сировини). Для виготовлення двох видів продукції П1 та П2 використовуються три види сировини S1, S2, S3. Запаси сировини, норми витрат сировини на виготовлення одиниці продукції кожного виду та дохід від одиниці продукції кожного виду наведені в таблиці:

Вид сировини	Запаси сировини	Витрати сировини на виготовлення одиниці продукції
П1	П2
S1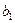
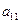
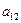
S2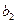
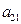
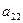
S2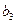
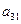
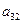
Дохід від одиниці продукції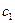

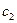
Необхідно знайти такий план виробництва продукції, який забезпечить найбільший сумарний дохід.

Побудуємо математичну модель задачі. Позначимо:

х₁, х₂ – загальна кількість продукції П₁ та П₂;

Z – сумарний дохід, який отримаємо від реалізації всієї продукції П₁ та П₂.

Запишемо цільову функцію задачі. Дохід від реалізації одиниці продукції П₁ становить с₁, а всього цієї продукції плануємо випустити х₁ одиниць, тому перемноживши с₁ на х₁, отримаємо весь дохід, який матимемо від реалізації всієї продукції. Аналогічно дохід від реалізації продукції П₂ становитиме с₂х₂. Додамо ці два доданки (с₁х₁+с₂х₂) і отримаємо весь дохід від реалізації всієї продукції П₁ та П₂. Оскільки ми хочемо отримати найбільший дохід, то будемо знаходити максимальне значення цільової функції:

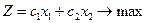
Тепер потрібно записати обмеження задачі. Нам відомо, скільки ресурсів кожного виду затрачається на виготовлення одиниці продукції кожного виду. Так, на виготовлення одиниці продукції П₁ ресурсу (сировини) S1 витрачаємо а₁₁, всього продукції П₁ плануємо виготовити 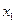одиниць. Перемножимо а₁₁ на 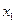і отримаємо ту кількість ресурсу S1, яка піде на виготовлення всієї продукції П₁. Цього ж ресурсу S1 на виготовлення одиниці продукції П₂ затрачаємо а₁₂, а плануємо виготовити х₂ одиниць продукції П₂, тому, коли перемножимо а₁₂ на х₂, будемо мати кількість ресурсу S1, затрачену на виготовлення всієї продукції П₂. Якщо додамо а₁₁ х₁ та а₁₂х₂, то отримаємо сумарні витрати ресурсу S1 на виготовлення всієї продукції П₁ та П₂. Але запас кожного виду ресурсу обмежений iвикористати більше, ніж ми маємо, не можемо. Запас ресурсу S1 становить 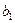. Тому обмеження з використання ресурсів матимуть вигляд:

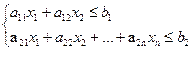
Очевидно, що невідомі 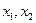не можуть бути від’ємними. Причому рівність нулю однієї з них означає, що даний вид продукції виготовляти недоцільно.

Ми отримали таку задачу лінійного програмування:

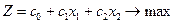(3.4)

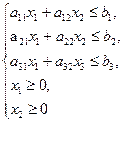(3.5)

Функція (3.4) - це цільова функція або функція мети, (3.5) - система обмежень задачі, причому перші три обмеження (3.5) називають основними обмеженнями, а останні два - природними чи економічними.

2) Узагальнена модель оптимального планування.Розглянемо загальну модель оптимального планування. Припустимо, що планується організувати випуск продукції r видів за допомогою т можливих технологій. Для цього використовується п видів виробничих ресурсів (матеріалів, обладнання, праці, сировини тощо). Введемо позначення: i - індекс ресурсу, 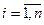; j – індекс технології, 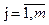; l - індекс виду продукції, 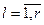; 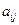- витрати ресурсу і-го виду на одиницю часу роботи технологічної лінії виду j; 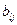- вихід продукції виду l за одиницю часу роботи технологічної лінії виду j; 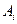- обсяг запасів ресурсів i-го виду; 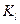- коефіцієнт, який відображає частку продукції виду l в загальному обсязі кінцевої продукції; 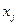- час роботи технологічної лінії виду j; Z - загальний обсяг кінцевої продукції.

Тоді узагальнена модель оптимального планування матиме вигляд: знайти такий план { 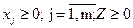}, який забезпечить

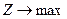
при виконанні обмежень:

а) за обсягом ресурсів:

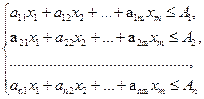(3.6)

б) за структурою кінцевої продукції

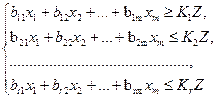(3.7)

3) Задача про складання кормового раціону.

В кормовий раціон для відгодівлі великої рогатої худоби (ВРХ) входять п’ять видів кормів К_h К₂, К₃, К₄ та К₅. Для забезпечення заданого приросту ваги тварини повинні споживати поживні речовини Р₁,Р₂ та Р₃. Мінімальна кількість поживних речовин, потрібних тваринам, а також вміст кількості одиниць поживних речовин в 1 кг корму та вартість 1 кг корму наведені в таблиці.

Необхідно скласти добовий раціон споживання ВРХ таким чином, щоб затрати на нього були мінімальними.

Поживні речовини	Мінімальна кількість поживних речовин	Кількість одиниць поживних речовин в 1 кг корму
Р1	К2	К3	К4	К5
Р1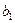
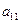
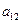
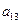
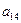
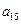
Р2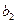
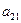
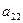
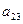
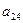
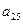
Р3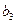
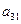
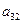
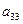
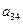
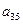
Вартість 1 кг корму	с1	с2	С3	С4	С5

Побудуємо математичну модель задачі. Введемо позначення: х_і - кількість корму (кг) К_і в раціоні (і=1, 2, 3, 4, 5); Z - вартість добового раціону.

Оскільки вартість одного кілограма корму становить с_і aзагальна кількість корму і-гoвиду, що потрібна для відгодівлі ВРХ становить х_і кг (і=1, 2, 3, 4, 5), то перемноживши с_і на х_і i додавши ці добутки, отримаємо вартість добового раціону відгодівлі ВРХ: Z = c₁x₁+c₂x₂+c₃x₃+c₄x₄+c₅x₅. Для побудови обмежень задачі перемножимо 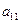- кількість поживних речовин Р₁, що містяться в 1кг корму К₁на загальну кількість цього корму х₁і так по всіх видах кормів, щоб в результаті отримати загальну кількість поживних речовин, отриманих від усіх п’яти кормів, а мінімальна кількість поживних речовин повинна становити відповідно 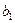, , 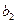,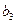тому обмеження з першого, другого та третього видів поживних речовин матимуть вигляд 3.9:

Ми отримали математичну модель задачі про кормовий раціон:

Цільова функція

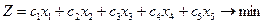(3.8)

Обмеження

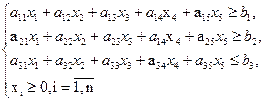(3.9)

4) Задача про раціональний розкрій матеріалів.

Розглянемо умови задачі. Значна частина матеріалів надходить на підприємство певними одиницями стандартних розмірів. Для використання його доводиться розрізати на частини, щоб отримати заготовки потрібних розмірів. Виникає проблема мінімізації відходів матеріалів.

Для побудови математичної моделі задачі введемо позначення. Нехай:

m – кількість різних заготовок;

B_i – план випуску заготовок і-го виду;

n - кількість різних способів (варіантів) розкрою стандартного матеріалу;

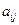– число заготовок і-го виду, одержаних за допомогою j-го способу розкрою;

с_j – величина відходів при j-му варіанті розкрою.

Схематично задачу можна представити у вигляді таблиці:

Варіант (спосіб) розкрою	Вихід заготовок з одиниці матеріалу	Відходи
1-го виду	2-го виду	…	m-го виду
			…
			…
…	…	…	…	…	…
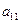
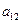
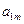
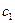
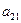
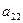
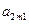
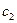
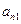
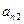
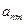
N			…		cn
План випуску заготовок	B1	B2	…	Bm

Через невідому x_j позначимо кількість одиниць вихідного матеріалу, які потрібно розрізати j-тим способом, а через Z – загальну кількість відходів.

Кількість заготовок i-го виду, одержана за всіма варіантами розкрою становитиме 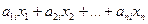, а нам потрібно цих заготовок в кількості B_i одиниць. Тому в якості обмеження з i-того виду заготовок буде рівність:

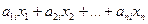=B_i .

В загальному випадку математична модель задачі раціонального розкрою матеріалу матиме вигляд:

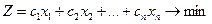(3.10)

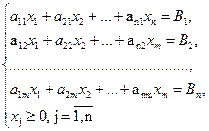(3.11)

Існуючі методи розв’язування задач лінійного програмування передбачають певні вимоги до системи основних обмежень (3.2), тому розрізняють дві стандартні форми запису задач лінійного програмування:

І-ша - з обмеженнями-рівняннями;

ІІ-га - з обмеженнями-нерівностями.

Запишемо задачу лінійного програмування в першій стандартній формі:

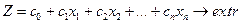(3.12)

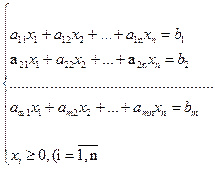(3.13)

Розв’язати задачу (3.12)-(3.13) - означає знайти такі розв’язки системи рівнянь (3.13), при яких цільова функція (3.12) набуває екстремального значення.

Задача ЛП записана в другій стандартній формі має вигляд:

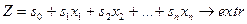(3.14)

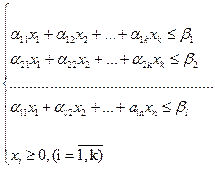(3.15)

Знайти розв’язок задачі, записаної в другій стандартній формі означає знайти такі розв’язки системи нерівностей (3.15), при яких цільова функція (3.14) набуває екстремального значення.