Двоїстий симплекс-метод
Розглянемо метод знаходження опорних планів, в якому використовується поняття двоїстості. Ми знаємо, що двоїстою задачею до задачі:
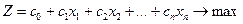
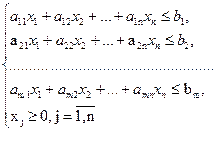
або у векторно-матричній формі:
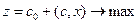
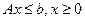
є задача:
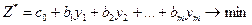
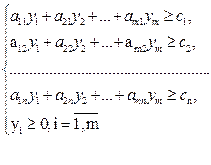
або у векторно-матричній формі:
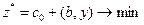
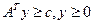
де АТ- матриця, транспонована до А;
(с,х), (b,y) - скалярні добутки відповідних векторів.
Якщо пряму задачу привести до канонічного виду і заповнити симплекс-таблицю, то ми бачимо, що стовпчики прямої задачі стануть рядками двоїстої, і навпаки. Тому нема потреби окремо розв’язувати вихідну задачу, а окремо - двоїсту, оскільки розв’язки обох можна знайти за одними й тими ж симплекс-таблицями, пам’ятаючи, що невідомим однієї задачі відповідають стовпчики, а невідомим другої - рядки.
Спочатку розглянемо, як можна використати поняття двоїстості для зведення прямої задачі до канонічної, причому основною задачею тут є зведення системи обмежень до канонічної форми, оскільки базисних невідомих в оптимізуючій формі завжди можна позбутися, виразивши їх через вільні з системи обмежень і підставивши в цільову функцію. З цієї простої причини ми не будемо звертати увагу на рядок оптимізуючої форми до тих пір, доки не отримаємо опорного плану.
Нехай в нас є задача, в базисі якої деякі плани від’ємні. Тоді ті базисні невідомі, що мають від’ємні плани, повинні бути виключені з базису.
Припустимо, що невідома хkмає від’ємний план ( 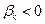 ). Розглянемо k-тий рядок. Якщо в ньому всі члени додатні (за винятком
). Розглянемо k-тий рядок. Якщо в ньому всі члени додатні (за винятком 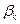 ), то двоїста задача, а разом з нею і вихідна не мають розв’язку через необмеженість форми.
), то двоїста задача, а разом з нею і вихідна не мають розв’язку через необмеженість форми.
В іншому випадку виділяємо стовпчики, в яких числа k-горядка від’ємні. Для кожного з виділених стовпчиків складаємо відношення елементів стовпця «План» до елементів виділених стовпців ( 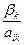 ) за принципом: додатні до додатних, від’ємні до від’ємних, і вибираємо найменші відношення, які позначимо через
) за принципом: додатні до додатних, від’ємні до від’ємних, і вибираємо найменші відношення, які позначимо через 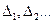 , а числа нульового рядка відповідних стовпчиків через
, а числа нульового рядка відповідних стовпчиків через 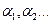 .
.
До базису вводимо вільну невідому, для якої (при знаходженні максимуму цільової функції):
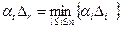
Дата добавления: 2016-07-22; просмотров: 2320;











