Основні елементарні функції

1. Лінійна функція 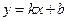. Область визначення функції (-∞, +∞), область зміни функції (-∞, +∞). Графік – пряма лінія(-∞, +∞). Кутовий коефіцієнт k дорівнює tgφ, де φ – кут між позитивним напрямком вісі Ох та прямою. Ця функція монотонна: зростає при k>0 та убуває при k<0.

2. Функція 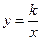визначена при всіх значеннях х за виключенням точки х=0. Область зміни функції – інтервали (-∞, 0), (0, +∞). Графік – гіпербола. Функція в кожному з інтервалів (-∞, 0) та (0, +∞) монотонна: зростає при k<0 та убуває при k>0. Функція виражає обернену пропорційну залежність між х та у. Функція непарна. Гіпербола симетрична відносно початку координат. Вісі координат є асимптотами гіперболи.

3.Функція 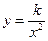. Ця функція визначена при будь-якому значенні х, крім точки х=0. Область зміни функції – інтервали (-∞, 0), (0, +∞). Графік – гіпербола. Функція в інтервалі (-∞, 0) при k>0 зростає, при k<0 зростає. Функція парна. Вісі координат є асимптотами гіперболи.

4. Показникова функція 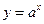(а>0) визначена на всій числовій вісі, область зміни функції (0, +∞). При а>1 функція монотонно зростаюча, при а<1 функція монотонно спадаюча. Вісь Ох є асимптотою. В якості основи цієї функції часто використовують число е 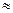2,71828…В цьому випадку функція називається експонентою.

5. Логарифмічна функція 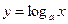(при а>0 та а 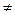1). Функція визначена при х>0. Область зміни функції(-∞, +∞) монотонна (зростає при а>1, убуває при а<1). Графік завжди проходить через точку (1;0). Вісь ординат є асимптотою для графіку. В якості основи функції а часто використовується число е 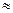2,71828… В цьому випадку функція називається натуральним логарифмом і позначається .

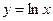6. Степенева функція з будь-яким раціональним показником 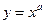. Розглянуті вище функції: х, 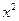, , 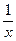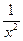є частковими випадками цієї функції.