Частные случаи движения точки

Движение точки с постоянной по модулю скоростью называют равномерным, т.е. 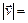const или 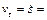const. Следовательно,

при криволинейном движении

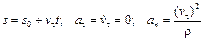; (1.13)

при прямолинейном движении, например, вдоль оси x

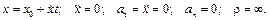(1.14)

Движение, при котором касательное ускорение точки не изменяется,называют равнопеременным, т.е. 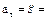const. Следовательно,

при криволинейном движении

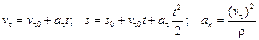, (1.15)

при прямолинейном движении

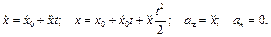(1.16)

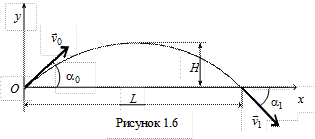
Пример. Движение снаряда в вертикальной плоскости (рис. 1.6) описывают уравнениями: x = 300 t, м; y = 400 t – 5t², м, где t – время, с.

Определить:

– траекторию, скорость и ускорение снаряда в начальный и конечный моменты времени;

– высоту подъема снаряда над уровнем горизонта H и дальность обстрела L;

– радиус кривизны траектории в ее начальной, конечной и наивысшей точках.

Решение

Найдем уравнение траектории, исключив из уравнения движения y = 400 t – 5t² (м) время t. Сначала из уравнения x = 300 t определим t = 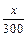, а затем получим уравнение траектории в следующем виде: 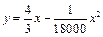. Траекторией снаряда в координатах х и у вертикальной плоскости является парабола.

Вычислим проекции скорости и ускорения снаряда на координатные оси:

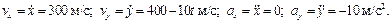
Определим их значения в начальный момент времени t = 0:

;

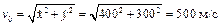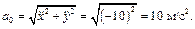
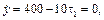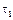Высоту подъема снаряда над уровнем горизонта можно определить, исследовав на экстремум функции y(t) по переменной t. Это означает, что с точки зрения кинематики проекция скорости точки на ось y в рассматриваемый момент времени должна быть равна нулю. Тогда где – время подъёма снаряда на максимальную высоту, 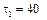с. Подставляя данное значение времени в выражение для y, получим y_max = H = y(40) = 8 км. Дальность обстрела определим из условия, что в момент падения снаряда функция y(t) принимает нулевое значени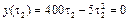е , где 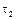– время полета снаряда. Корень этого квадратного уравнения, соответствующий падению снаряда на землю, 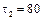с, откуда дальность полета х_max = х(80) = 24 км.

Теперь, зная время полета снаряда, можно определить его скорость и ускорение в конце полета. Подставляя время 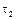в выражение для проекции скорости снаряда на ось y, получим 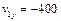м/с. Проекции скорости и ускорения на ось x не зависят от времени и постоянны в течение полета. Таким образом, снаряд движется с постоянным ускорением, равным 10 м/с² и направленным вертикально вниз, а его скорость в конце полета равна по модулю скорости в начале его 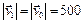м/с и составляют с осью x одинаковые углы .

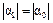Для определения радиуса кривизны перейдем к кинематическим характеристикам движения снаряда в естественной системе отсчета.

Вначале найдем касательное ускорение по формуле

,

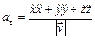а затем вычислим его для начального момента времени

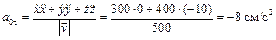
и для конечного

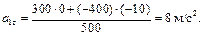
Теперь можно посчитать нормальное ускорение по формуле 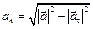, а затем и 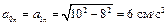. Поскольку радиус кривизны траектории входит в формулу 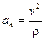, то

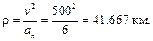
Радиусы кривизны траектории в начале и в конце полета одинаковы. В наивысшей точке траектории

;

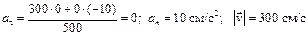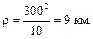
Как видно из приведенного примера, уравнения движения точки содержат все необходимое для исследования характеристик ее движения в любой момент времени.

Вопросы для самоконтроля

1. В чем заключаются задачи кинематики точки и абсолютно твердого тела?

2. Какие способы применяют для задания движения точки?

3. Как определяют скорость точки при различных способах задания ее движения?

4. Как определяют ускорение точки при различных способах задания ее движения?