Алгоритм процесу збору та інтерпретації даних

При вивченні маркетингової інформації досить важливим є питання щодо процесу збору та інтерпретації маркетингової інформації. Алгоритм цього процесу представлено на рис. 2.1.

Рисунок 2.1 – Процес збору та інтерпретації маркетингової інформації

Вихідним етапом процесу збору та інтерпретації маркетингової інформації є визначення проблеми, яку необхідно дослідити. Слід зазначити, що правильне визначення проблеми – це 50 % майбутнього успіху.

Після цього встановлюється міра поінформованості (як у даний час, так і можливої). Для цього можуть бути використані такі критерії:

· об’єктивні: кількість (повнота), релевантність (змістовність, значимість), точність (однозначність), надійність, зрозумілість, актуальність, пристосованість до мети дослідження;

· суб’єктивні: ризикованість, характер (стресовий чи заспокійливий), вмотивованість;

· економічні (затрати);

· пов’язані з існуючими обмеженнями: захищеність, допустимість інформаційних контактів, допустимість засобів зв’язку, міра захисту інформації.

Третій етап процесу – опрацювання концепції збору інформації. Він полягає у розробці проекту збору інформації, методів її збору, альтернативних варіантів (повне чи вибіркове, разове або періодичне, одно- чи багаторазове дослідження).

Четвертий етап – збір інформації та перевірка правильності її вибору. Критеріями такої перевірки вторинних даних є характеристика установи, що збирала дані, відповідність інформації поставленим завданням, методи та час збору, актуальність зібраних даних. У разі недостатності зібраної інформації переходять до польових досліджень (збору первинної інформації).

Після цього зібрані дані підлягають обробці (зведенню у відповідні таблиці, представленню у вигляді діаграм, графіків тощо).

Наступний етап процесу – аналіз даних. Для адекватної оцінки результатів дослідження на промислових підприємствах в межах МІС доцільно організовувати центр первинної обробки інформації, в якому на базі розрахунку середніх величин визначатимуться попередні результати, їх точність та достовірність.

До статистичних оцінок параметрів розподілу відповідей груп респондентів належать: середня арифметична зважена, групова дисперсія сукупності, внутрігрупова дисперсія сукупності, міжгрупова дисперсія, загальна дисперсія.

Середня арифметична зважена ( 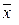) – середня сукупності з урахуванням загального обсягу ознаки, що варіює, та її частоти:

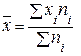, (2.1)

де 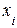– варіанта ознаки, що варіює; 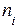– частота ознаки, що варіює.

Групова дисперсія сукупності ( 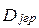) – дисперсія значень ознаки, яка приналежить групі, відносно групової середньої:

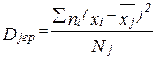, (2.2)

де 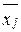– групова середня групи; 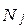– обсяг групи j.

Внутрігрупова дисперсія сукупності ( 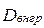) – середня арифметична групових дисперсій, яка зважена за обсягами груп.

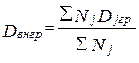, (2.3)

Міжгрупова дисперсія 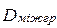– дисперсія групових середніх відносно загальної середньої.

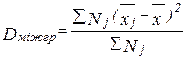, (2.4)

де 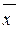– загальна середня сукупності.

Загальна дисперсія 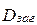– дисперсія значень ознаки всієї сукупності відносно загальної середньої.

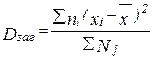, (2.5)

Загальна дисперсія дорівнює сумі внутрігрупової та міжгрупової дисперсій ( = + ).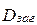

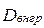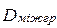Приклад.Сукупність складається з двох груп (див. табл. 2.2.):

Таблиця 2.2 – Вихідні дані

Група 1	Група 2
варіанта ознаки,	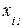частота ознаки,	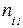варіанта ознаки,	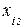частота ознаки,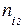
		–	–
Разом Σ	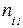	Разом Σ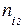

Розрахувати: 1) групові дисперсії сукупності;

2) внутрігрупову дисперсію сукупності;

3) міжгрупову дисперсію;

4) загальну дисперсію.

Розв’язання:

1) визначаємо середні арифметичні зважені груп та сукупності:

,

;

;

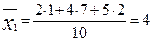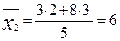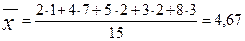2) визначаємо групові дисперсії сукупності:

;

;

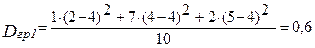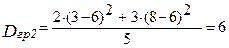3) розраховуємо внутрігрупову дисперсію:

;

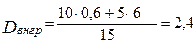4) знаходимо міжгрупову дисперсію:

;

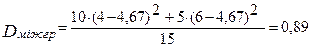5) визначаємо загальну дисперсію сукупності:

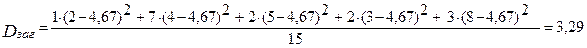
Перевірка: 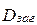= 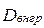+ 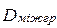= 2,4 + 0,89 = 3,29.

Достовірність та точність результатів МД оцінюють за допомогою довірчого інтервалу. Оскільки правдиве значення величини, що вимірюється, дорівнює її математичному очікуванню, визначення достовірності результатів МД зводиться до визначення довірчого інтервалу для математичного очікування.

Довірчий інтервал для математичного очікування має вигляд:

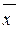‑ δ < < + δ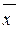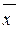, (2.6)

де δ – точність оцінки ( 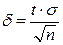); t – аргумент, якому відповідає значення функції Лапласа, що дорівнює 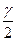; γ – надійність оцінки; 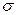– середнє квадратичне відхилення; n – обсяг вибірки.

Приклад. Випадкова величина має нормальний розподіл з відомим середнім квадратичним відхиленням 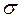=3. Знайти довірчий інтервал для оцінки невідомого математичного очікування за вибірковими середніми 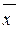, якщо обсяг вибірки складає n = 36 організацій, надійність оцінки завдана на рівні γ = 0,95.

Розв’язання:

1) знаходимо параметр t за таблицею значень функції Лапласа:

2Ф(t) = γ = 0,95; Ф(t) = 0,475; t = 1,96;

2) визначаємо точність оцінки:

;

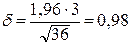3) довірчий інтервал матиме вигляд:

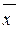( ‑ 0,98; 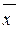+ 0,98).

Точність результатів МД характеризується середнім квадратичним відхиленням 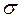випадкових помилок, тому необхідно знайти такий довірчий інтервал:

s (1 – q) < 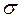< s (1 + q), (2.7)

де s – „виправлене” середнє квадратичне відхилення; q – величина зі статистичної таблиці значень q = q ( γ , n).

„Виправлене” середнє квадратичне відхилення s розраховується як корінь квадратний з „виправленої” дисперсії, яку отримують множенням вибіркової дисперсії на дріб 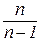, тобто вибіркову дисперсію „виправляють” таким чином, щоб її математичне очікування було рівним генеральній дисперсії.

Приклад. За 15 рівноточними вимірами знайдено „виправлене” середнє квадратичне відхилення s = 0,12. Знайти точність вимірів з надійністю γ = 0,95.

Розв’язання:

1) за вихідними даними визначаємо q = q (0,95;15) = 0,46;

2) довірчий інтервал матиме вигляд:

0,12 (1 – 0,46) < 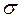<0,12 (1 + 0,46),

0,0648 < 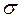<0,1752.

Після проведення наведених вище розрахунків маркетингова інформація інтегрується, виходячи з поставлених цілей у відповідні висновки і рекомендації. Останні формуються у відповідному звіті, який захищається перед замовниками. Це – останній етап процесу.