Катушка индуктивности

Катушкой индуктивности (индуктивным элементом) называется элемент электрической цепи, для которого напряжение пропорционально скорости изменения тока или магнитного потока (производной по времени).

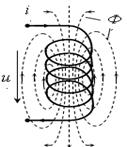
Если через катушку индуктивности (рис. 4.3, а) пропустить синусоидальный ток 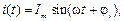то он создаст переменный магнитный поток Ф, пронизывающий витки катушки. По закону электромагнитной индукции, на зажимах катушки этот переменный поток наведет синусоидальное напряжение:

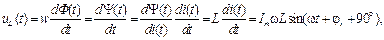(4.1)

где w – число витков катушки;

Y – потокосцепление;

Y = wФ;

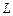– индуктивность;

;

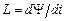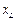– реактивное индуктивное сопротивление;

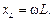
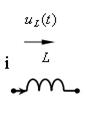а	б	в
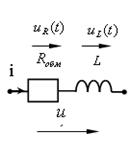
Рис. 4.3. Катушка индуктивности

Индуктивность L характеризует способность индуктивного элемента запасать энергию в магнитном поле катушки индуктивности 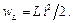Индуктивность катушки индуктивности измеряется в Генри (Гн).

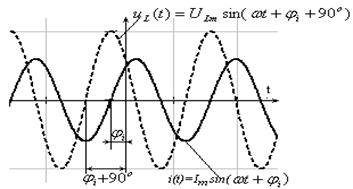
Из соотношения (4.1) видно, что протекающий через катушку индуктивности ток i(t) отстает от напряжения 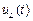на угол 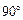(рис. 4.4).

t Рис. 4.4. Диаграммы тока и напряжения для катушки индуктивности

На рис. 4.3, б показана низкочастотная схема замещения катушки индуктивности, состоящая из индуктивности L и активного сопротивления обмоткиR_обм. Переменный ток, протекая по виткам катушки, создает в проводниках тепловые потери мощности:

p = i² ∙ R_обм.

Если сопротивлением обмотки R_обм можно пренебречь, то такую катушку считают идеальной индуктивностью (рис. 4.3, в). Для высоких частот в схеме замещения необходимо также учитывать межвитковую емкость катушки.

Из (4.1) следует, что при заданном напряжении 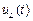ток 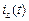можно найти в соответствии с выражением:

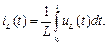(4.2)

Для установившегося режима работы и гармонического приложенного напряжения 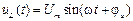ток через катушку индуктивности определится соотношением:

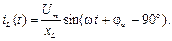(4.3)

Конденсатор

Конденсатором (емкостным элементом) называется элемент, для которого протекающий ток пропорционален скорости изменения заряда или напряжения (производной по времени).

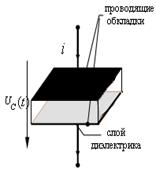
Конденсатор является элементом электрической цепи, имеющим две проводящие обкладки, между которыми находится слой диэлектрика (рис. 4.5, а). Если к зажимам конденсатора подключить источник синусоидального напряжения 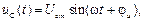то на его обкладках возникнет изменяющийся во времени электрический заряд q(t), т.е. через конденсатор будет протекать электрический ток:

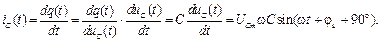(4.4)

а	б	в
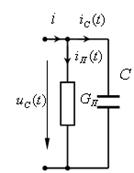
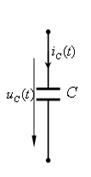
Рис. 4.5. Конденсатор

В (4.4) С = dq/dU_c – емкость конденсатора, которая определяет зависимость изменения величины заряда на обкладках конденсатора от изменения напряжения, приложенного к его обкладкам. х_с = 1/(ωС) – реактивное емкостное сопротивление. Емкость конденсатора измеряется в Фарадах (Ф).

Из соотношения (4.4) видно, что ток через конденсатор i(t) опережает напряжение 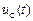на угол 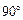(рис. 4.6).

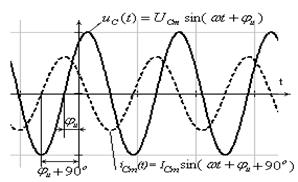
Рис. 4.6. Диаграммы тока и напряжения для конденсатора

Основной особенностью конденсатора является его способность запасать энергию в электрическом поле W_c = CU_c²/2. Кроме того, в конденсаторе имеют место тепловые потери энергии в диэлектрике и обкладках, а также происходит запас энергии в магнитном поле. На рис. 4.5, б показана низкочастотная схема замещения конденсатора, состоящая из параллельного соединения емкости C и активного сопротивления с проводимостью G_П, учитывающей потери в диэлектрике и обкладках. Если потерями можно пренебречь, то конденсатор будет представлять собой идеальную емкость (рис. 4.5, в).

Из (4.4) следует, что напряжение 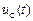при заданном токе 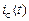можно найти по формуле:

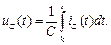(4.5)

Для установившегося режима работы при гармоническом токе 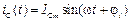в (4.5) напряжение на конденсаторе имеет вид:

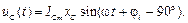(4.6)