Частотные характеристики электрических цепей
Под входной характеристикой цепи при гармоническом воздействии понимают зависимость его входного комплексного сопротивления 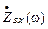 или проводимости
или проводимости 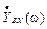 от частоты.
от частоты.
Комплексной передаточной функцией по напряжению 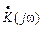 называется зависимость отношения комплексного действующего значения выходного напряжения к комплексному действующему значению входного напряжения от частоты. Функция
называется зависимость отношения комплексного действующего значения выходного напряжения к комплексному действующему значению входного напряжения от частоты. Функция 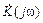 представляется двумя зависимостями: АЧХ (амплитудная частотная характеристика) – зависимость модуля от частоты и ФЧХ – зависимость его фазы от частоты. Во многих случаях частотные характеристики цепи могут меняться в широких пределах, поэтому удобнее их представлять в логарифмическом масштабе (логарифмическая частотная характеристика или ЛАЧХ). Оценивается ЛАЧХ в децибелах (дБ). Для пассивных цепей данная частотная характеристика называется ослаблением цепи. При расчете частотных характеристик линейных цепей реактивные сопротивления катушки индуктивности и конденсатора записываются как функции частоты:
представляется двумя зависимостями: АЧХ (амплитудная частотная характеристика) – зависимость модуля от частоты и ФЧХ – зависимость его фазы от частоты. Во многих случаях частотные характеристики цепи могут меняться в широких пределах, поэтому удобнее их представлять в логарифмическом масштабе (логарифмическая частотная характеристика или ЛАЧХ). Оценивается ЛАЧХ в децибелах (дБ). Для пассивных цепей данная частотная характеристика называется ослаблением цепи. При расчете частотных характеристик линейных цепей реактивные сопротивления катушки индуктивности и конденсатора записываются как функции частоты: 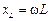 и
и 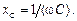 Предполагается, что сопротивления резистивных элементов R от частоты не зависят.
Предполагается, что сопротивления резистивных элементов R от частоты не зависят.
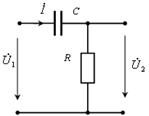
Рассмотрим расчет частотных характеристик на примере схемы с последовательным соединением элементов R и C (рис. 4.11).
|
| Рис. 4.11. Схема RC-цепи |
Входное комплексное сопротивление цепи:
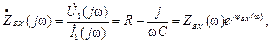 (4.21)
(4.21)
где 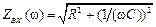 и
и 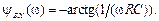
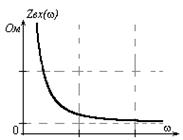
На рис. 4.12 изображены графики входных характеристик 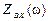 и
и 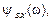 рассчитанных по формулам (4.21).
рассчитанных по формулам (4.21).
Комплексная передаточная функция по напряжению имеет вид:
 (4.22)
(4.22)
АЧХ и ФЧХ определятся соотношениями:
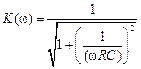 и
и 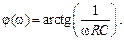 (4.23)
(4.23)
 а
а
|  б
б
|
| Рис. 4.12. Частотные характеристики последовательной RC-цепи |
Для качественной оценки частотной характеристики введем параметр – постоянную времени τ = RC. Тогда формулы частотных характеристик будут иметь следующий вид:
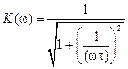 и
и 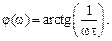 (4.24)
(4.24)
ЛАЧХ определяется выражением:
 (4.25)
(4.25)
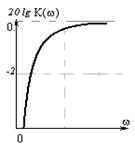
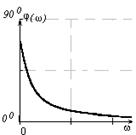
На рис. 4.13 представлены графики частотных характеристик АЧХ, ЛАЧХ и ФЧХ, рассчитанных по формулам (4.22)–(4.24).
 а
а
|  б б
|  в
в
|
| Рис. 4.13. Частотные передаточные характеристики |
Дата добавления: 2020-10-14; просмотров: 1118;











