Связь стеганопреобразования и возмущений спектра и собственных векторов матрицы контейнера
Любое стегопреобразование возмущает спектр матрицы ОС и (или) ее ортонормированные СВ. Установим связь между этими возмущениями и характеристиками СМ, а также свойствами СС.
Пусть 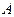 – произвольная симметричная
– произвольная симметричная 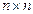 матрица, модули СЗ которой попарно различны. Тогда, как уже говорилось в лекции 4, для нее существует единственное нормальное спектральное разложение. Из единственности упомянутого разложения вытекает, что любое преобразование, в частности стеганопреобразование, матрицы ЦИ формально представляется в виде возмущения ее спектра и (или) СВ, которые и определяются нормальным спектральным разложением.
матрица, модули СЗ которой попарно различны. Тогда, как уже говорилось в лекции 4, для нее существует единственное нормальное спектральное разложение. Из единственности упомянутого разложения вытекает, что любое преобразование, в частности стеганопреобразование, матрицы ЦИ формально представляется в виде возмущения ее спектра и (или) СВ, которые и определяются нормальным спектральным разложением.
Назовем абсолютной отделенностью СЗ 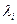 матрицы
матрицы 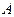 число, которое определяется в соответствии с формулой:
число, которое определяется в соответствии с формулой:
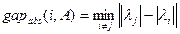 .
.
Можно показать, что для обеспечения высокой вероятности сохранения надежности восприятия СС для заданного контейнера СМ должен обеспечивать малую норму (в частности, Фробениуса, СМН) матрицы возмущений при стеганопреобразовании. Для этого погружение ДИ в контейнер целесообразно проводить таким образом, чтобы при представлении стеганопреобразования в виде возмущений спектра и СВ матрицы ОС, возмущенные СВ отвечали малым по модулю СЗ или СЗ, которые имеют малые абсолютные отделенности, а возмущение СЗ (не имеет значения, каких именно) были малые. Чем меньше возмущение СЗ, абсолютные отделенности и модули СЗ, которые отвечают возмущенным СВ, тем больше вероятность сохранения надежности восприятия СС.
Теорема. Пусть результатом стеганопреобразования являются возмущения СВ матрицы ОС. Достаточным условием обеспечения малой чувствительности полученного СС к разным возмущениям и, как следствие, увеличение устойчивости процесса декодирования ДИ, является соответствие возмущенных СВ собственным значениям, которые имеют большую абсолютную отделенность. Абсолютная отделенность СЗ, которые отвечают возмущенным СВ, является мерой чувствительности полученного СС к возмущающим воздействиям.
Доказательство. Пусть матрица 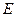 - возмущение
- возмущение 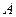 , вызванное возмущением матрицы СВ
, вызванное возмущением матрицы СВ 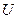 из СР (3) вследствие стеганопреобразования. Тогда:
из СР (3) вследствие стеганопреобразования. Тогда: 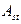 =
= 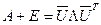 , где
, где 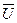 - возмущенная матрица
- возмущенная матрица 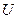 . Поскольку результатом стеганопреобразования является изменение некоторых СВ матрицы ОС, то чувствительность СС будет определяться чувствительностью возмущенных СВ. Пусть
. Поскольку результатом стеганопреобразования является изменение некоторых СВ матрицы ОС, то чувствительность СС будет определяться чувствительностью возмущенных СВ. Пусть 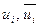 - исходный и возмущенный нормированные СВ, которые отвечают СЗ
- исходный и возмущенный нормированные СВ, которые отвечают СЗ 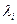 , а
, а 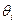 - угол между ними. Тогда заключение теоремы следует из соотношения:
- угол между ними. Тогда заключение теоремы следует из соотношения:
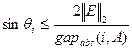 . (5.6)
. (5.6)
Действительно, согласно (5.6) СВ тем меньше будет чувствительным к возмущениям, чем больше абсолютная отделенность его СЗ.
Следствие. Если результатом стеганопреобразования является возмущение матрицы 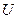 вследствие изменения СВ, для которых СЗ имеют малую абсолютную отделенность, то СС будет чувствительным к возмущающим воздействиям, что может привести к недостаточной эффективности декодирования ДИ в такому СМ.
вследствие изменения СВ, для которых СЗ имеют малую абсолютную отделенность, то СС будет чувствительным к возмущающим воздействиям, что может привести к недостаточной эффективности декодирования ДИ в такому СМ.
Вывод: Надежность восприятия СС, его чувствительность к возмущающим воздействиям однозначно определяются возмущениями СЗ и СВ матрицы ОС при стеганопреобразовании. Исходя из расположения и абсолютных значений этих возмущений можно сделать априорные оценки для свойств любого СМ, а также провести сравнение нескольких СМ.
Вопросы
- Основные требования к стеганографическому алгоритму.
- В чем заключается проблема априорной оценки свойств произвольного стеганографического алгоритма?
- Формальное представление произвольного стеганопреобразования.
- Почему любое стеганопреобразование можно представить как аддитивное погружение дополнительной информации в пространственной области контейнера?
- Спектральное разложение матрицы контейнера. Свойства, особенности.
- Полные наборы параметров. Свойства собственных значений и собственных векторов матрицы цифрового изображения.
- Каким образом матрицу произвольного цифрового изображения можно представить в симметричном виде?
- Стеганографический метод, использующий спектральное разложение матрицы контейнера.Модификация базового алгоритма с целью увеличения скрытой пропускной способности.
- Что такое абсолютная отделенность собственного значения?
- Связь стеганопреобразования и возмущений собственных значений матрицы контейнера.
- Связь стеганопреобразования и возмущений собственных векторов матрицы контейнера.
- Что является мерой чувствительности к возмущающим воздействиям стеганосообщения? Почему?
- Когда стеганосообщение оказывается чувствительным/нечувствительным к возмущающим воздействиям?
Литература
1. Кобозєва А.А. Аналіз захищеності інформаційних систем / Кобозєва А.А., Хорошко В.А., Мачалін І.О. – К.: Вид.ДУІКТ, 2010. – 316 с.
2. Кобозева А.А. Анализ информационной безопасности / А.А.Кобозева, В.А.Хорошко. – К.: Изд. ГУИКТ, 2009. – 251 с.
3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с.
4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.
5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
6. Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.
7. Грибунин В.Г. Цифровая стеганография / В.Г.Грибунин, И.Н.Оков, И.В.Туринцев. — М.: Солон-Пресс, 2002. — 272с.
8. Стеганография, цифровые водяные знаки и стеганоанализ : [монография] / А.В. Аграновский, А.В. Балакин, В.Г. Грибунин, С.А. Сапожников. — М.: Вузовская книга, 2009. — 220 с.
9. Кобозева А.А. Применение сингулярного и спектрального разложения матриц в стеганографических алгоритмах / А.А.Кобозева // Вісник Східноукр-го нац-го ун-ту ім. В.Даля. — 2006. — №9(103), ч.1. — С.74—82.
10. Конахович Г.Ф. Компьютерная стеганография. Теория и практика / Г.Ф.Конахович, А.Ю.Пузыренко. — К.: МК — Пресс, 2006. — 288 с.
11. Кобозева А.А. Учет свойств нормального спектрального разложения матрицы контейнера при обеспечении надежности восприятия стегосообщения / А.А.Кобозева, Е.А.Трифонова // Вестник НТУ «ХПИ». — 2007. — №18. — С.81—93.
12. Кобозева А.А. Оценка чувствительности стегосообщения к возмущающим воздействиям / А.А.Кобозева, Е.В.Нариманова // Системні дослідження та інформаційні технології. – 2008. - №3. – С. 52-65.
13. Хорошко В.А. Основи комп‘ютерної стеганографії: навчальний посібник для студентів і аспірантів / В.А.Хорошко, О.Д.Азаров, М.Є.Шелест, Ю.Є.Яремчук. — Вінниця: ВДТУ, 2003. -143 с.
14. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с.
15. Алиев, А.Т. Оценка стойкости систем скрытой передачи информации / А.Т. Алиев, А.В. Балакин // Известия ТРТУ. Тематический выпуск. Материалы VII Международной научно-практической конференции «Информационная безопасность». — Таганрог: Изд-во ТРТУ, 2005. — №4 (48). — С. 199–204.
16. Корольов, В.Ю. Планування досліджень методів стеганографії та стеганоаналізу / В.Ю. Корольов, В.В. Поліновський, В.А. Герасименко, М.Л. Горінштейн // Вісник Хмельницького національного університету. — 2011. — № 4. — С. 187–196.
17. Miller, A. Least Significant Bit Embeddings: Implementation and Detection [Электронный ресурс]: Computer Science Honors Thesis. – 2012. – Режим доступа: http://aaronmiller.in/thesis.
18. Chandramouli, R. Analysis of LSB based Image Steganography Techniques / R. Chandramouli, N. Memon // Proceedings of ICIP, Thessaloniki, Greece, October 7-10, 2001. — 2001. — Vol.3. — PP. 1019–1022.
19. Кобозева, А.А. Общий подход к анализу состояния информационных объектов, основанный на теории возмущений / А.А. Кобозева // Вісник Східноукраїнського національного університету ім. В. Даля. — 2008. — №8(126), Ч.1. — С. 72–81.
Лекция 6. Общий подход к оценке свойств стеганографического алгоритма
(продолжение)
План
1. Оценка свойств и сравнение стеганографических методов.
2. Примеры использования нового метода.
Дата добавления: 2016-07-22; просмотров: 1679;











