Стеганографический метод, использующий спектральное разложение матрицы контейнера
Для иллюстрации пункта 3) предыдущего параграфа рассмотрим пример конкретного стеганометода.
Пусть матрица  размерности
размерности 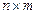 отвечает контейнеру. Разобьем ее на квадратные
отвечает контейнеру. Разобьем ее на квадратные 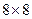 -блоки. Пусть
-блоки. Пусть 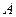 - матрица одного из таких блоков, которая, как правило, не является симметричной.
- матрица одного из таких блоков, которая, как правило, не является симметричной.
Блоку 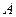 исходного изображения ставятся в соответствие две симметричные
исходного изображения ставятся в соответствие две симметричные 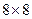 -матрицы
-матрицы 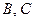 по правилу (2.4):
по правилу (2.4):
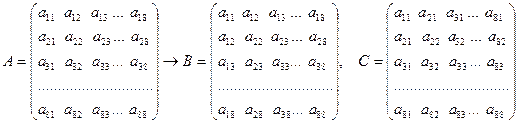 (5.3)
(5.3)
Пусть спектральные разложения 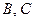 – это
– это
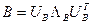 ,
, 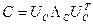 . (5.4)
. (5.4)
Погружаемое секретное сообщение рассматривается как некоторая бинарная последовательность 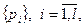 элементы которой принадлежат множеству
элементы которой принадлежат множеству 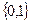 . Основные этапы предлагаемого стеганоалгоритма, который далее будем называть базовым и обозначать BSPECTR, сформулируем следующим образом:
. Основные этапы предлагаемого стеганоалгоритма, который далее будем называть базовым и обозначать BSPECTR, сформулируем следующим образом:
- Матрица
 основного сообщения разбивается на квадратные блоки размера
основного сообщения разбивается на квадратные блоки размера 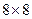 ;
; - Пусть
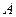 - очередной блок, полученный на предыдущем шаге, используемый для погружения ДИ. Согласно (5.3) по
- очередной блок, полученный на предыдущем шаге, используемый для погружения ДИ. Согласно (5.3) по 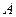 строим матрицы
строим матрицы 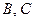 , каждая из которых используется для погружения одного бита ДИ;
, каждая из которых используется для погружения одного бита ДИ; - Для матриц
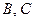 строим спектральные разложения (5.4).
строим спектральные разложения (5.4). - Пусть
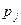 - очередной бит секретного сообщения, встраивание которого происходит в В. Для погружения определяющим является количество положительных собственных значений используемой матрицы: четное количество этих значений отвечает
- очередной бит секретного сообщения, встраивание которого происходит в В. Для погружения определяющим является количество положительных собственных значений используемой матрицы: четное количество этих значений отвечает 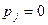 , нечетное -
, нечетное - 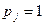 . Если количество положительных собственных значений и
. Если количество положительных собственных значений и 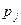 соответствуют друг другу, как предложено выше, то погружение произведено. Предположим, что нужного соответствия нет. Тогда из всех собственных значений
соответствуют друг другу, как предложено выше, то погружение произведено. Предположим, что нужного соответствия нет. Тогда из всех собственных значений 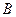 выбирается минимальное по модулю. Пусть это -
выбирается минимальное по модулю. Пусть это - 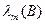 . Это значение возмущается в соответствии с формулой:
. Это значение возмущается в соответствии с формулой:
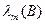 = -
= - 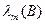 , (5.5)
, (5.5)
при этом величина возмущения 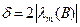 и имеет минимально возможное значение при модификации спектра, определяемой формулой (5.5).
и имеет минимально возможное значение при модификации спектра, определяемой формулой (5.5).
Четность количества положительных собственных значений изменится на противоположную, что и требуется.
- Аналогичные действия проделываются с очередным битом секретного сообщения и
матрицей 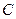 . Таким образом, в один блок
. Таким образом, в один блок 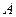 в итоге погружается два бита ДИ (по сравнению с несимметричным вариантом пропускная способность увеличивается в 2 раза).
в итоге погружается два бита ДИ (по сравнению с несимметричным вариантом пропускная способность увеличивается в 2 раза).
- После погружения формируется блок
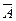 , соответствующий блоку
, соответствующий блоку 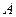 , по следующему правилу:
, по следующему правилу:
а) матрицы 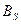 и
и 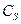 строятся в виде произведений
строятся в виде произведений 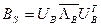 ,
, 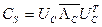 ,
,
где 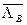 и
и 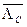 - матрицы собственных значений, отличающиеся от
- матрицы собственных значений, отличающиеся от 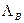 и
и 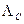
за счет возможных модификаций, проделанных на этапе 4 в соответствии с (5.5);
б) обозначим элементы матриц 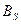 и
и 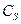 как
как 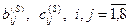 , соответственно.
, соответственно.
Тогда
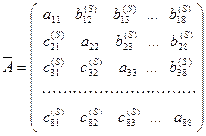 .
.
- Значения элементов блока
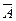 могут, вообще говоря, не принадлежать множеству
могут, вообще говоря, не принадлежать множеству
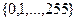 . Поэтому для окончательного формирования блока
. Поэтому для окончательного формирования блока 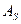 СС, отвечающего
СС, отвечающего 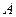 , необходимо:
, необходимо:
а) провести округление вещественных элементов 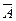 до ближайших целых по
до ближайших целых по
известному правилу. Результат обозначим 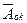 ;
;
б) обеспечить нахождение значений элементов 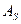 в пределах [0, 255]. Для этого
в пределах [0, 255]. Для этого
используется следующая операция, которую ниже будем называть усечением:
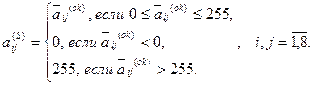
Здесь 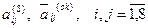 , - элементы
, - элементы 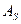 и
и 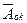 соответственно.
соответственно.
- Если пересылаемое сообщение не погружено полностью, переходим к очередному блоку
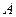 , используемому для погружения ДИ, возвращаемся к этапу 2. В противном случае, формирование СС завершено.
, используемому для погружения ДИ, возвращаемся к этапу 2. В противном случае, формирование СС завершено.
После того, как шаги 1-7 будут проделаны для всех блоков основного сообщения  , которые выбраны для погружения ДИ, будет сформировано стеганосообщение
, которые выбраны для погружения ДИ, будет сформировано стеганосообщение 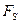 , которое затем пересылается по каналу связи адресату. Нужно заметить, что выбор используемых для погружения блоков ОС может быть осуществлен различными способами в соответствии с секретным ключом (в предельном случае могут использоваться все блоки
, которое затем пересылается по каналу связи адресату. Нужно заметить, что выбор используемых для погружения блоков ОС может быть осуществлен различными способами в соответствии с секретным ключом (в предельном случае могут использоваться все блоки  ).
).
Декодирование ДИ осуществляется в соответствии с алгоритмом, основные шаги которого следующие:
- Матрица
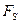 стеганосообщения разбивается на квадратные блоки размера
стеганосообщения разбивается на квадратные блоки размера 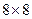 ;
; - Для каждого из блоков
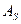 , полученных на предыдущем шаге, несущих в себе ДИ в соответствии с секретным ключом, строим матрицы
, полученных на предыдущем шаге, несущих в себе ДИ в соответствии с секретным ключом, строим матрицы 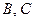 аналогично (5.3);
аналогично (5.3); - Строим спектральное разложение матриц
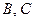 . В каждом из спектральных разложений считаем количество положительных собственных значений; в зависимости от четности этих чисел делаем вывод о двух погруженных битах секретной информации.
. В каждом из спектральных разложений считаем количество положительных собственных значений; в зависимости от четности этих чисел делаем вывод о двух погруженных битах секретной информации. - Для очередного блока
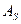 возвращаемся к этапу 2.
возвращаемся к этапу 2.
Порядок встраивания (извлечения) бит может быть частью секретного ключа. Например, для всех блоков 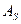 , участвующих в погружении ДИ, бит, встроенный (извлеченный) в матрицу
, участвующих в погружении ДИ, бит, встроенный (извлеченный) в матрицу 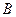 , предшествует биту, встроенному (извлеченному) в
, предшествует биту, встроенному (извлеченному) в 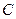 ; или для блоков
; или для блоков 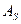 , номер которых кратен 3, бит, встроенный (извлеченный) в
, номер которых кратен 3, бит, встроенный (извлеченный) в 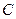 , предшествует встроенному (извлеченному) в
, предшествует встроенному (извлеченному) в 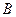 , а для всех остальных – наоборот и т.д.
, а для всех остальных – наоборот и т.д.
Модификация базового алгоритма с целью увеличения пропускной способности. Для предложенного выше базового стегоалгоритма каждый из блоков исходного контейнера  используется для пересылки двух бит секретного сообщения. Если матрица
используется для пересылки двух бит секретного сообщения. Если матрица  имела размерность
имела размерность 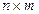 , то количество блоков после ее разбиения определялось как
, то количество блоков после ее разбиения определялось как 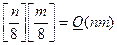 . Тогда максимальная длина пересылаемого сообщения (при условии, что в погружении участвуют все полученные при разбиении
. Тогда максимальная длина пересылаемого сообщения (при условии, что в погружении участвуют все полученные при разбиении  блоки) равна
блоки) равна 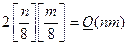 .
.
Как показывает вычислительный эксперимент, в спектрах матриц 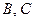 , как правило, наименьшее по модулю собственное значение мало отличается от собственного значения, модуль которого следует за минимальным. Таким образом, надежность восприятия после погружения ДИ заметно не пострадает, если изменение знака произойдет не у одного собственного значения матрицы, модуль которого минимальный, а у двух с наименьшими модулями. Это замечание дает нам возможность построения модификации базового алгоритма, различающей не два состояния матриц
, как правило, наименьшее по модулю собственное значение мало отличается от собственного значения, модуль которого следует за минимальным. Таким образом, надежность восприятия после погружения ДИ заметно не пострадает, если изменение знака произойдет не у одного собственного значения матрицы, модуль которого минимальный, а у двух с наименьшими модулями. Это замечание дает нам возможность построения модификации базового алгоритма, различающей не два состояния матриц 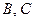 (количество положительных собственных значений четно, нечетно), которые соответствуют двум буквам в алфавите передаваемого сообщения - 0,1, а три – количество положительных собственных значений при делении на три дает в остатке 0, 1, 2, что позволит расширить алфавит ДИ до трех знаков, например, 0, 1, 2, а значит увеличить пропускную способность. Обозначим такой модифицированный алгоритм SPECTR2. Обобщение можно продолжить, используя возможность изменения знаков сразу 3, 4 или более собственных значений, модули которых мало отличаются друг от друга (ниже для таких модификаций алгоритма ВSPECTR используются обозначения SPECTR3, SPECTR4 и т.д.).
(количество положительных собственных значений четно, нечетно), которые соответствуют двум буквам в алфавите передаваемого сообщения - 0,1, а три – количество положительных собственных значений при делении на три дает в остатке 0, 1, 2, что позволит расширить алфавит ДИ до трех знаков, например, 0, 1, 2, а значит увеличить пропускную способность. Обозначим такой модифицированный алгоритм SPECTR2. Обобщение можно продолжить, используя возможность изменения знаков сразу 3, 4 или более собственных значений, модули которых мало отличаются друг от друга (ниже для таких модификаций алгоритма ВSPECTR используются обозначения SPECTR3, SPECTR4 и т.д.).
Заметим, что количество положительных собственных значений, используемое при погружении и декодировании ДИ, является целой величиной, а, значит, не зависит напрямую от особенностей машинной арифметики, что является важной положительной характеристикой предложенных алгоритмов.
Результаты вычислительного эксперимента.Вычислительный эксперимент проводился в среде MATLAB в условиях идеального канала связи. Для реализации алгоритма в качестве ОС брались многочисленные монохромные изображения. Для демонстрации результатов использованы изображения POUT (рис.5.1(а)), CAMERAMAN, MRI (рис.5.2(а,б)). Погружаемое сообщение генерировалось случайным образом, однако все результаты, приведенные в работе, соответствуют такому секретному сообщению, для погружения которого необходимо было изменение знаков всех предназначаемых для этого собственных значений во всех полученных блоках. Такой вариант был выбран намеренно, чтобы представить наихудшую из имеющихся возможностей с точки зрения как визуализации получаемого стеганосообщения, так и декодирования. Результаты погружения ДИ во все полученные блоки изображения POUT в соответствии с предложенным выше алгоритмом и его модификациями представлены на рис.5.1(б,в,г). Как и предполагалось, надежность восприятия стеганосообщения сохраняется не только при применении BSPECTR. Мало заметные артефакты начинают появляться лишь при применении SPECTR4 (рис.5.1(в)), становясь четкими при использовании SPECTR5 (рис.5.1(г)), что соответствует обязательной модификации пяти минимальных по модулю собственных значений в каждом блоке. При проведении вычислительного эксперимента встречались изображения, где применение даже SPECTR5 визуально было незаметно.
Важнейшей характеристикой любого стеганоалгоритма является эффективность декодирования ДИ. Некоторые результаты декодирования в проведенном вычислительном эксперименте отражены в табл.5.1. Конечно приведенные результаты зависят от выбранного изображения и спектральных свойств используемых матриц, о чем уже говорилось выше, однако необходимо отметить, что базовый алгоритм дает малый процент ошибок на любом изображении. Что касается SPECTR2, SPECTR3 и т.д., то эффективность декодирования ДИ этими алгоритмами уступает эффективности базового. Это является своеобразной «платой» за повышение в них скрытой пропускной способности.


а б


в г
Рисунок 5.1- Изображение POUT и его преобразование: а - исходное ЦИ; б – СС, сформированное при погружении во все блоки ОС за счет обязательной модификации одного СЗ; в – СС, сформированное при погружении во все блоки ОС за счет обязательной модификации четырех СЗ; г - СС, соответствующее обязательной модификации пяти СЗ
Таблица 5.1 – Количество ошибок при декодировании, выраженное в процентах, для различных изображений в идеальном канале связи
| Алгоритм Изобра жение | ВSPECTR | SPECTR2 | SPECTR3 |
| POUT | |||
| CAMERAMAN | |||
| MRI |

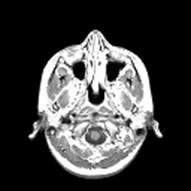
а б


в г
Рисунок 5.2 – ЦИ, использованные для демонстрации результатов вычислительного эксперимента: а –CAMERAMAN; б –MRI; в – СС, сформированное на основе CAMERAMAN при помощи алгоритма SPECTR3 с модификацией диагонального элемента; г - СС, сформированное на основе CAMERAMAN при помощи алгоритма SPECTR3
Дата добавления: 2016-07-22; просмотров: 1726;











