Тема 8. Статистическое изучение взаимосвязи социально – экономических явлений

Измерение связи

Все явления общественной жизни взаимосвязаны и взаимо­обусловлены. Задача статистики состоит в том, чтобы выявить и измерить связи и зависимости между изучае­мыми явлениями.

Взаимосвязанные признаки подразделяются на фактор­ные (под их воздействием изменяются другие, зависящие от них признаки) и результативные.

Связи по степени тесноты могут быть функциональны­ми (при которых определенному значению факторного признака соответствует строго определенное значение ре­зультативного признака; для выявления такой связи дос­таточно одного наблюдения), статистическими (когда одному и тому же значению факторного признака могут со­ответствовать несколько значений результативного при­знака; эти связи проявляются в массе случаев и при том - в среднем). Функциональные связи иначе называются пол­ными, а статистические — неполными или корреляцион­ными.

Корреляционная зависимость проявляется только в средних величинах и выражает числовое соотношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании и убывании другой.

Корреляционная связь является свободной, неполной и неточной связью. Например, себестоимость величины продукции зависит от уровня производительности труда: чем выше производительность труда, тем ниже ce6eстоимость. Но себестоимость зависит также и от ряда других факторов: стоимости сырья и материалов, топлива, элект­роэнергии, их расхода на единицу продукции, цеховых общезаводских расходов и т.д. Поэтому нельзя утверж­дать, что при повышении производительности труда, допустим, на 10% себестоимость снизится также на 10%. Может случиться, что, несмотря на рост производитель­ности труда, себестоимость не только не снизится, но даже несколько повысится, если на нее окажут более сильное влияние действующие в обратном направлении другие факторы.

По направлению различа­ют прямую и обратную связь. Если с увеличением аргу­мента х функция у также увеличивается без всяких еди­ничных исключений, то такая связь называется полной прямой связью. Если с увеличением аргумента х функция у уменьшается без всяких единичных исключений, то та­кая связь называется полной обратной. Кроме того, в виде исключений, которые, однако, не нарушают общей тен­денции, встречается частичная связь — прямая или обрат­ная. Когда признаки варьируют независимо друг от друга, говорят о полном отсутствии связи.

По аналити­ческому выражению корреляционная связь может быть прямолинейной и криволинейной. Прямолинейной назы­вается связь, когда величина явления изменяется прибли­зительно равномерно в соответствии с изменением вели­чины влияющего фактора. Математически прямолинейная связь может быть выражена уравнением прямой:

V=a₀ +a₁х, (8.1)

которое называется линейным уравнением регрессии.

Если происходит неравномерное изменение явления в связи с изменением величины влияющего фактора, то та­кая связь называется криволинейной. Математически кри­волинейная зависимость может быть выражена уравнени­ем криволинейной связи. В экономическом анализе для ее выражения часто пользуются уравнением параболы вто­рого порядка:

V = а₀ + a₁ х + а₂х² (8.2)

Уравнение криволинейной связи может быть выражено и в виде дробной функции:

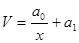(8.3)

показательной функции:

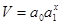(8.4.)

Однако корреляционные связи могут быть выражены лишь приблизительно, в то время как функциональные связи имеют точное аналитическое выражение.