Корреляционный анализ

Корреляционный анализ решает две основные задачи.

Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь. Это очень важно, так как от правильного выбора формы связи зависит конечный результат изучения взаимосвязи между признаками.

Вторая задача состоит в измерении тесноты, т.е. меры связи между признаками с целью установить степень влияния данного фактора на результат. Она решается математически путем определения параметров корреляционного уравнения.

Затем проводятся оценка и анализ полученных результатов при помощи специальных показателей корреляционного метода (коэффициентов детерминации, линейной и множественной корреляции и т.д.), а также проверка существенности связи между изучаемыми признаками.

Определяющая роль в выборе формы связи между явлениями принадлежит теоретическому анализу. Так, например, чем больше размер основного капитала предприятия (факторный признак), тем больше при прочих равных условиях оно выпускает продукции (результативный признак). С ростом факторного признака здесь, как правило, равномерно растет и результативный, поэтому зависимость между ними может быть выражена уравнением прямой Y = а₀ + а₁x , которое называется линейным уравнением регрессии.

Параметр а₁называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу. При х=0 а₀ = Y. Увеличение количества внесенных удобрений приводит, при прочих равных условиях, к росту урожайности, но чрезмерное внесение их без изменения других элементов к дальнейшему повышению урожайности не приводит, а, наоборот, снижает ее. Такая зависимость может быть выражена уравнением параболы Y = а₀ + а₁x + а₂x^2..

Параметр а₂характеризует степень ускорения или замедления кривизны параболы, и при а₂ > 0 парабола имеет минимум, а при а₂ < 0 — максимум. Параметр а₁ характеризует угол наклона кривой, а параметр а₀ — начало кривой.

Однако с помощью теоретического анализа не всегда удается установить форму связи. В таких случаях приходится только предполагать о наличии определенной формы связи. Проверить эти предположения можно при помощи графического анализа, который используется для выбора формы связи между явлениями, хотя графический метод изучения связи применяется и самостоятельно.

Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически — в виде уравнения — и придавать ей количественное выражение. Рассмотрим применение приемов корреляционного анализа на конкретном примере.

Допустим, что между стоимостью основного капитала и выпуском продукции существует прямолинейная связь, которая выражается уравнением прямой Y = а₀ + а₁x. Необходимо найти параметры а₀и a₁что позволит определить теоретические значения Y для разных значений х. Причем а₀и a₁должны быть такими, чтобы было достигнуто максимальное приближение к первоначальным (эмпирическим) значениям теоретических значений Y. Эта задача решается при помощи способа наименьших квадратов, основное условие которого сводится к определению параметров а₀и a₁таким образом, чтобы å (у_i - Y) ² = min .

Математически доказано, что условие минимума обеспечивается, если параметры а₀и a₁определяются при помощи системы двух нормальных уравнений, отвечающих требованию метода наименьших квадратов:

åy=na₀ +a₁åx

åxy=a_0*åx²(8.10)

Первое уравнение есть сумма всех первоначальных уравнений. Второе получается умножением обеих частей уравнения прямой на один и тот же множитель. Математически доказано, что условие å (у_i - Y) ² = min соблюдается, если в качестве такого множителя принять значение факторного признака, т.е. если уравнение прямой умножить на x.

Кроме рассмотренных функций связи в экономическом анализе часто применяются степенная, показательная и гиперболическая функции.

Степенная функция имеет вид Y = а₀ х^а1. Параметр a₁ степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1 %. При х = 1 а₀ =.Y .

Для определения параметров степенной функции вначале ее приводят к линейному виду путем логарифмирования: lg y = lg a₀ + а₁ lg x₁ , а затем строят систему нормальных уравнений:

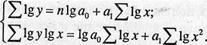(8.11)

Решив систему двух нормальных уравнений, находят логарифмы параметров логарифмической функции а₀ и а₁а затем и сами параметры а₀ и а₁ При помощи степенной функции определяют, например, зависимость между фондом заработной платы и выпуском продукции, затратами труда и выпуском продукции и т.д.

Если факторный признак x растет в арифметической прогрессии, а результативный у — в геометрической, то такая зависимость выражается показательной функцией Y = а_{0 *}а₁² . Для определения параметров показательной функции ее также вначале приводят к линейному виду путем логарифмирования: lg у = lg а₀ + х lg a₁, а затем строят систему нормальных уравнений:

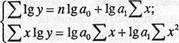(8.12)

Вычислив соответствующие данные и решив систему двух нормальных уравнений, находят параметры показательной функции а_ои а_1.

В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы:

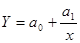(8.13)

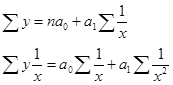И здесь задача заключается в нахождении параметров а₀ и a_t при помощи системы двух нормальных уравнений:

(8.14)

При помощи гиперболической функции изучают, например, связь между выпуском продукции и себестоимостью, уровнем издержек обращения (в % к товарообороту) и товарооборотом в торговле, сроками уборки и урожайностью и т.д.

Таким образом, применение различных функций в качестве уравнения связи сводится к определению параметров уравнения по способу наименьших квадратов при помощи системы нормальных уравнений.

В малых совокупностях значение коэффициента регрессии подвержено случайным колебаниям. Поэтому возникает необходимость в определении достоверности коэффициента регрессии. Достоверность коэффициента регрессии определяется так же, как и в выборочном наблюдении, т.е. устанавливаются средняя и предельная ошибки для выборочной средней и доли. Средняя ошибка коэффициента регрессии определяется по формуле:

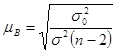
(8.15)

где s₀² — случайная дисперсия; s²— общая дисперсия, п - число коррелируемых пар.

<21 22 232425 26 27 >

Дата добавления: 2016-07-22; просмотров: 2571;