Основные приемы изучения взаимосвязей

Для изучения, измерения и количественного выраже­ния взаимосвязей между явлениями статистикой приме­няются различные методы, такие как: метод сопоставле­ния параллельных рядов, балансовый, графический, ме­тоды аналитических группировок, дисперсионного и кор­реляционного анализа.

Метод параллельных рядов заключается в том, что полученные в результате сводки и обработки материалы располагают в виде параллельных рядов и сопоставляют их между собой для установления характера и тесноты связи.

Балансовый метод состоит в том, что данные взаимо­связанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдель­ными ее частями были равны, т.е. чтобы был баланс. Ба­лансовый метод используется для характеристики взаи­мосвязи между производством и распределением про­дуктов, денежными доходами и расходами населения и т.д. Почти все внутренние и внешние хозяйственные свя­зи выражаются в виде балансов.

Метод аналитических группировок. Сущность метода аналитических группировок состоит в том, что единицы статистической совокупности группируются, как правило, по факторному признаку и для каждой группы рассчиты­вается средняя или относительная величина по результа­тивному признаку. Затем изменения средних или относи­тельных значений результативного признака сопоставляются с изменениями факторного признака для выявления характера связи между ними.

Дисперсионный анализ дает прежде всего возможность определить значение систематической и случайной вариа­ций в общей вариации, а также установить роль интересу­ющего нас фактора в изменении результативного призна­ка.

Для характеристики тесноты корреляционной связи между признаками в аналитических группировках меж­групповую дисперсию сопоставляют с общей. Это сопо­ставление называется корреляционным отношением и обозначается:

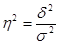(8.5.)

Оно характеризует долю вариации результативного признака, вызванной действием факторного признака, положенного в основание группировки. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем ближе корреляционное отноше­ние к 1, тем большее влияние оказывает факторный при­знак на результативный. Если же факторный признак не влияет на результативный, то вариация, обусловленная им, будет равна нулю (d ²= 0) и корреляционное отношение также будет равно нулю (h²=0), что говорит о полном отсутствии связи. И наоборот, если результативный при­знак изменяется только под воздействием одного фактор­ного признака, то вариация, обусловленная этим призна­ком, будет равна общей вариации (h²=h²) и корреляци­онное отношение будет равно единице (h² = 1), что го­ворит о существовании полной связи.

Дисперсионный анализ позволяет не только опреде­лить роль случайной и систематической вариаций в об­щей вариации, но и оценить достоверность вариации, обнаруженной методом аналитических группировок. Опре­деление достоверности вариации дает возможность с за­данной степенью вероятности установить, вызвана ли меж­групповая вариация признаком, положенным в основание группировки, или она является результатом действия слу­чайных причин. Для оценки существенности корреляци­онного отношения пользуются критическими значениями корреляционного отношения h²при разных уровнях веро­ятности или значимости a.

Уровень значимости — это достаточно малое значе­ние вероятности, отвечающее событиям, которые в дан­ных условиях исследования будут считаться практически невозможными. Появление такого события считается ука­занием на неправильность начального предположения. Чаще всего пользуются уровнями a = 0,05 или a = 0,01. Критические значения корреляционного отношения содержатся в специальных таблицах.

В этих таблицах распределение h² при случайных вы­борках зависит от числа степеней свободы факторной и случайной дисперсии. Число степеней свободы фактор­ной дисперсии равно:

К₁=m-1 (8.6.)

где m — число групп, а для случайной дисперсии:

K₁=n – m (8.7.)

где п — число вариант; m — число групп.

При проверке существенности связи чаще пользуются критерием Фишера, потому что при больших числах сте­пеней свободы его табличные значения мало изменяются в отличие от корреляционного отношения, которое требу­ет более громоздких таблиц. Критерий Фишера представ­ляет собой отношение межгрупповой дисперсии к сред­ней из внутригрупповых дисперсий, исчисленных с уче­том числа степеней свободы:

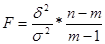(8.8)

Для этих отношений составляются таблицы, по кото­рым можно определить, какая величина F при данном числе степеней свободы по факторной вариации (K₁) и остаточной вариации (К₂) дает основание утверждать с определенной вероятностью (например, 0,95; 0,99), что положенный в основание группировки признак является существенным, или не дает такого основания, и, следо­вательно, группировочный признак является несуществен­ным.

Зная корреляционное отношение, можно определить критерий Фишера по следующей формуле:

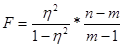(8.9.)

Подобный дисперсионный анализ может проводиться при группировке по одному факторному признаку или при комбинационной группировке по двум и более факторам.
В таком случае необходима оценка достоверности влияния не только каждого положенного в основание группировки фактора в отдельности, но и результата их взаимо­действия. Последний определяется как разность между эффектом совместного влияния двух группировочных признаков и суммой эффектов влияния каждого из этих факторных признаков, взятых в отдельности. Это осложняет расчеты суммы квадратов отклонений и числа степеней свободы вариации. Но сам принцип дисперсионного анализа, основанный на сопоставлении факторной дисперсии со случайной для оценки достоверности результатов ста­тистической группировки, остается применим независимо от числа признаков группировки.