Структурные характеристики вариационного ряда распределения
Для характеристики величины варьирующего признака пользуютсяструктурными величинами. Они бывают двух видов:
· Мода –наиболее часто встречающееся значение ряда (варианты). Мода применяется, например, при определении размера обуви, одежды, пользующейся наибольшим спросом у покупателей.
Для дискретных рядов мода – это вариант, имеющий наибольшую частоту.
При расчете моды для интервального ряда необходимо вначале определить модальный интервал, т.е. интервал, который имеет наибольшую частоту, а затем значение модального признака. В этом случае моду рассчитывают по следующей формуле:
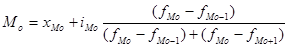 (5.21.)
(5.21.)
хмо – нижняя граница модального интервала;
iмо - величина модального интервала;
fмо – частота, соответствующая модальному интервалу;
fмо-1 – частота, предшествующая модальному интервалу;
fмо+1 – частота интервала, следующего за модальным.
Мода определяет непосредственно размер признака, свойственный, хотя и значительной части, но все же не всей совокупности. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.
· Медиана – значение элемента, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Медиана делит ряд на две равные части.
Медиана – значение признака у средней единицы ранжированного ряда. Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания единиц.
Для ранжированного ряда с нечетным числом единиц медианой будет являться варианта, расположенная в центре ряда. Для ранжированного ряда с четным числом единиц медиана определяется как среднее арифметическое из двух смежных вариант, находящихся в центре ряда.
В интервальных рядах для определения медианы необходимо:
1.расположить значение признака по ранжиру;
2.для ранжированного ряда определить сумму частот;
3.найти медианный интервал. Он будет находиться там, где полусумма накопленных частот больше или равна сумме частот.
Значение медианы находится по формуле:
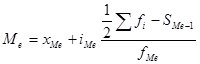 (5.22.)
(5.22.)
хме – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
iме – величина медианного интервала;
f /2 – полусумма частот ряда;
Sме-1 – сумма накопленных частот, предшествующих медианному интервалу;
fме – частота медианного интервала.
Медиана не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные результаты, чем при использовании других форм средних.
Вопросы для теоретического контроля знаний:
1. Что представляет собой вариация признака, от чего зависят ее размеры?
2. Что такое размах вариации? По какой формуле он исчисляется? В чем его недостаток?
3. Что представляет собой среднее линейное отклонение? Его формулы, недостатки.
4. Какие показатели называются дисперсией и средним квадратическим отклонением? По каким формулам они вычисляются?
5. Что представляет собой вариация альтернативного признака? Чему она равна?
6. Какие виды дисперсий Вы знаете?
7. Каковы основные свойства дисперсий?
8. Как вычисляются показатели вариации в интервальном ряду?
9. Как осуществляется изучение формы распределения?
10. Теоретические распределения в анализе вариационных рядов.
11. Структурные характеристики вариационного ряда распределения.
12. Что представляет собой мода и медиана?
13. Как вычисляется мода в дискретных и интервальных рядах?
14. Как вычисляется медиана в дискретных и интервальных рядах?
15. Что представляет собой правило сложения дисперсий? В чем его практическое значение?
16. Дайте определение эмпирического коэффициента детерминации. В чем его смысл?
17. Дайте определение эмпирического корреляционного отношения. В чем его смысл?
Примеры решения задач:
1.На основе данных (дискретный ряд) табл. 5.1. рассчитаем среднее линейное отклонение для дискретного ряда распределения.
Таблица 5.1.
Распределение учителей средних школ района по стажу работы
Стаж работы, лет 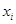
| Число учителей в % к итогу, 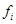
| 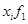
| 
| 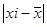
| 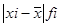
|
| -2 | |||||
| -1 | |||||
| Итогу | - |
Размах вариации стажа равен : R = xmax - xmin = 12 – 8 = 4 года.
Результаты вспомогательных расчетов даны в графах 3 – 5 табл.5.1.
Средний стаж работы определяем по формуле средней арифметической взвешенной : 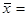 1000:100 = 10 лет
1000:100 = 10 лет
Отклонения индивидуальных значений стажа от средней с учетом и без учета знака содержатся в графах 4 и 5, а произведения отклонений по модулю на соответствующие частоты – в гр. 6.
Среднее линейное отклонение стажа работы учителей средних школ района:
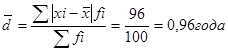
2. Рассчитаем дисперсию и среднее квадратическое отклонение для следующего ряда распределения (табл. 5.2.)
Таблица 5.2.
Распределение магазинов города по товарообороту во 2 квартале 2003г.
| Группы магазинов по величине товарооборота, тыс. руб. | Число магази
нов, 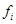
| Середина интерва
ла, тыс. руб., 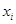
| 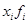
| 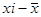
| 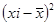
| 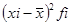
|
| А | ||||||
| 40 – 50 | 49,2 | 2420,64 | 4841,28 | |||
| 50 – 60 | -39,2 | 1536,64 | 6146,56 | |||
| 60 – 70 | -29,2 | 852,64 | 5968,48 | |||
| 70 – 80 | -19,2 | 368,64 | 3686,40 | |||
| 80 – 90 | -9,2 | 84,64 | 1269,60 | |||
| 90 – 100 | 0,8 | 0,64 | 12,80 | |||
| 100 – 110 | 10,8 | 116,64 | 2566,08 | |||
| 110 – 120 | 20,64 | 432,64 | 4759,04 | |||
| 120 – 130 | 30,8 | 948,64 | 5691,84 | |||
| 130 – 140 | 40,8 | 1164,64 | 4993,92 | |||
| Итого | - | - | 399936,00 |
При расчете вариации по интервальным рядам распределения необходимо сначала определить середины интервалов, а затем ввести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный ряд распределения.
Результаты вспомогательных расчетов для определения дисперсии и среднего и квадратического отклонения содержатся в графах 2 – 6 табл. 7.2.
Средний размер товарооборота определяется по средней арифметической взвешенной и составляет: 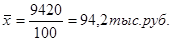
Дисперсия товарооборота:
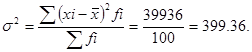
Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:
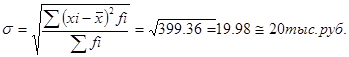
3. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 5.3. (аналитическая группировка)
Таблица 5.3.
Производительность труда двух бригад рабочих токарей
| 1 бригада | 2 бригада | ||||||
| № | Изготовлено деталей за час, шт. | 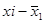
| 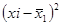
| № | Изготовлено деталей за час, шт. | 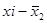
| 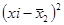
|
| -2 | -3 | ||||||
| -1 | -2 | ||||||
| -1 | |||||||
Для расчета групповых дисперсий вычислим среднее по каждой группе:
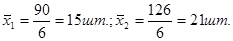
Промежуточные расчеты дисперсий по группам представлены в табл. 5.3. Подставив полученные значения в формулу, получим:
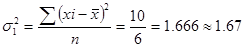
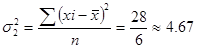
Средняя из групповых дисперсий:
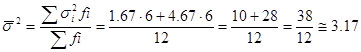
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
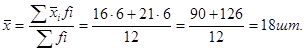
Теперь определим межгрупповую дисперсию:
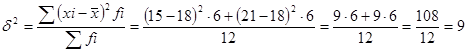
Задания для самостоятельной работы:
1. Определить групповые дисперсии доли, среднюю из групповых, межгрупповую и общую дисперсии доли по данным табл. 5.4.
Таблица 5.4.
Численность и удельный вес одной из категорий крупного рогатого скота фермерских хозяйств района
| Хозяйство | Удельный вес дойных коров, % | Всего коров |
| Итого |
2. Рассчитать коэффициент асимметрии и показатель эксцесса по данным о распределении фирм по стоимости основных фондов (табл. 5.5.)
Таблица 5.5.
Расчет коэффициента асимметрии
| Группы фирм по стоимости основных фондов, млн. руб., х | Количество фирм, fi |
| 0,5-1,0 | |
| 1,0-1,5 | |
| 1,5-2,0 | |
| 2,0-2,5 | |
| Итого |
3.Рассчитать моду и медиану по данным таблицы 5.6. (дискретный ряд).
Таблица 5.6.
Распределение обуви, проданной коммерческой фирмой в январе 2003г.
| Раз мер | 44 и более | Итого | ||||||
| Кол – во проданных пар, % к итогу |
4. ассчитать моду и медиану для интервального ряда распределения по данным таблицы 5.7.
Таблица 5.7.
Распределение семей города по размеру среднедушевого дохода в январе 2003г.
| Группы семей по размеру дохода, руб. | Число семей |
| До 500 | |
| 500 – 600 | |
| 600 – 700 | 1 700 |
| 700 – 800 | 2 500 |
| 800 – 900 | 2 200 |
| 900 – 1000 | 1 500 |
| Свыше 1000 | |
| Итого | 10 000 |
Литература:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 1996.- с.81-104.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Инфра – М, 2000. –с. 107-156.
3. Гусаров В.М. Статистика. М.: ЮНИТА – ДАНА, 2001. –с.71-85.
4. Общая теория статистики под ред.Спирина А.А. М.: Финансы и статистика, 1996.-с.101-124.
5. Статистика: курс лекций под ред. Ионина В.Г. Изд – во НГАЭИУ, М.: Инфра – М, 1997. –с.84-91.
6. Теория статистики под ред. Шмойловой Р.А. М.: Финансы и статистика, 2002. – с.176 – 221.
Дата добавления: 2016-07-22; просмотров: 5610;











