Относительные величины
Относительные величины представляют собой частное от деления двух статистических величин и характеризуют количественное отношение между ними.
При расчете относительных величин следует иметь в виду, что в числителе всегда находится показатель, отражающий изучаемое явление, а в знаменателе показатель, с которым проводится сравнение, принимаемый за базу сравнения или основание.
В зависимости от базы сравнения относительные величины могут быть выражены:
· в коэффициентах, база сравнения принимается за единицу и показывает во сколько раз изучаемое явление отличается от базы сравнения;
· в процентах, база сравнения принимается за 100;
· в промилле, база сравнения принимается за 1000;
· в продецимиле, база сравнения принимается за 10000000.
При расчете относительных величин необходимо обеспечить сопоставимость сравниваемых показателей.
В зависимости от задач относительные величины подразделяются:
· относительный показатель динамики
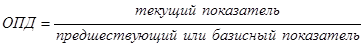 (4.2.)
(4.2.)
· относительный показатель планового задания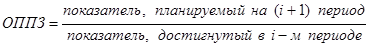 (4.3.)
(4.3.)
· относительный показатель выполнения плана 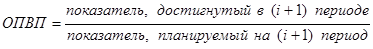 (4.4.)
(4.4.)
Между относительной величиной динамики, планового задания, выполнения плана существует взаимосвязь: показатель динамики представляет собой произведение планового задания на выполнение плана.
ОПД =ОППЗ *ОПВП) (4.5.)
· относительный показатель выполнения договорных обязательств
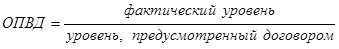 (4.6.)
(4.6.)
· относительный показатель структуры
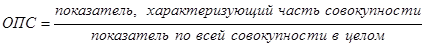 (4.7.)
(4.7.)
· относительный показатель интенсивности
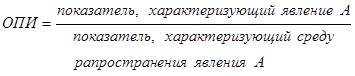
(4.8.)
· относительный показатель координации
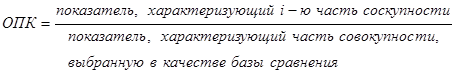 (4.9.)
(4.9.)
· относительный показатель сравнения
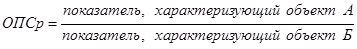
(4.10.)
4. Средние величины
Средняя величина – это обобщающая характеристика однородной совокупности явлений по определенному признаку.. Средняя величина выражает характерное, типичное значение признака у всех единиц. Средние величины используют для сравнения и выявления закономерностей.
Для того, что бы рассчитать любую среднюю величину необходимо соблюдать следующие требования:
1. средняя величина должна быть рассчитана только на основе массовых достоверных данных;
2. средняя величина будет объективна и типична, если она рассчитывается для качественно однородной совокупности;
3. числитель и знаменатель должны быть сравнимы.
Все средние величины объединяются в общей формуле средней степенной (при различной величине k):
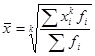 (4.11.)
(4.11.)
хi – отдельные значения изучаемого явления (вариант);
fi – частота значений признака (вес i – го варианта);
n – объем совокупности.
Из формулы степенной средней, придавая К различные значения, можно вывести формулу различных средних величин. Выделяют следующие степенные средние величины:
· Средняя арифметическая простая
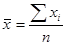 (4.12.)
(4.12.)
· Средняя арифметическая взвешенная
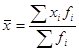 (4.13.)
(4.13.)
· Средняя гармоническая простая
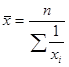 (4.14.)
(4.14.)
· Средняя гармоническая взвешенная
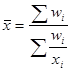 (4.15.)
(4.15.)
wi = xifi– произведение варианты на частоту.
· Средняя хронологическая
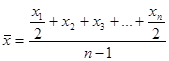 (4.16.)
(4.16.)
· Средняя геометрическая простая
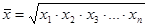 (4.17.)
(4.17.)
· Средняя геометрическая взвешенная
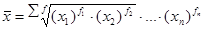 (4.18.)
(4.18.)
· Средняя квадратическая простая
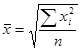 (4.19.)
(4.19.)
· Средняя квадратическая взвешенная
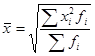 (4.20.)
(4.20.)
Вопросы для теоретического контроля знаний:
1. Что представляют статистические показатели?
2. Назовите основные виды статистических показателей.
3. Что такое абсолютные показатели и каково их значение?
4. В каких единицах измерения выражаются абсолютные статистические величины?
5. Что называется относительными показателями?
6. Какие виды относительных показателей Вы знаете?
7. Дайте определение средних показателей.
8. Какие виды средних применяются в статистике?
9. Средняя арифметическая и ее свойства.
10. Понятие и способы исчисления средней арифметической и средней гармонической.
Примеры решения задач:
1. Производство сахара–песка в РФ в январе – апреле 2000г.характеризуется следующими данными (табл. 4.1.)
| Месяц | Январь | Февраль | Март | Апрель |
| Объем производства, тыс. т |
Рассчитаем относительные показатели динамики с переменной и постоянной базой сравнения (см. формулу 4.2.):
| Переменная база сравнения (цепные показатели) | Постоянная база сравнения (базисные показатели) |
| 138 108 * 100% = 127, 8% | 138 108 * 100% = 127, 8% |
| 131 138 * 100% = 94,9% | 131 108 * 100% = 121,3% |
| 206 138 * 100% = 157,3% | 206 108 * 100% = 190,7% |
2. Предположим, оборот торговой фирмы в 2000г. составил 2,0 млрд. руб. Исходя из проведенного анализа складывающихся на рынке тенденций руководство фирмы считает реальным в следующем году довести оборот до 2,8 млрд. руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 140% (2,8 : 2,0 *100%). Предположим теперь, что фактический оборот фирмы за 2001г. составил 2,6 млрд. руб. Тогда относительный показатель реализации плана, определяемый как отношение фактически достигнутой величины к ранее запланированной, составит 92,9% (2,6 : 2,8 *100%).
3. По данным таблицы 4.2. рассчитаем среднюю заработную плату в целом по трем предприятиям АО.
Таблица 4.2.
Заработная плата предприятий АО
| Предприятие | Численность промышленно-производственного персонала, чел. | Месячный фонд заработной платы, тыс. руб. | Средняя заработная плата, руб. |
| А | |||
| 564,84 | |||
| 332,75 | |||
| 517,54 | |||
| Итого | 1415,13 | ? |
Предположим, что мы располагаем только данными гр. 1 и 2 табл. 4.2. Итоги этих граф содержат необходимые величины для расчета искомой средней. Воспользуемся формулой средней агрегатной:
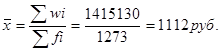
где, wi = xi fi
xi – вариант осредняемого признака
fi – вес признака
Если мы располагаем только данными о средней заработной плате и численности работников (гр. 1 и 3), то общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
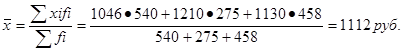
Можно рассчитать среднюю заработную плат в целом по трем предприятиям по формуле средней гармонической взвешенной:
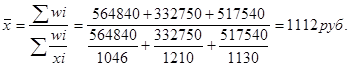
Задания для самостоятельной работы студентов:
1, По данным таблицы (4.3) рассчитать относительные показатели структуры
Таблица . 4.3.
Показатели валового внутреннего продукта РФ в 1 квартале 2000г.
| Показатели | Объем | |
| Трлн. руб. | % к итогу | |
| ВВП – всего | 508,0 | |
| В том числе: | ||
| производство товаров | 185,4 | |
| производство | 277,9 | |
| чистые налоги на продукты | 44,7 |
2. По данным таблицы 4.3. рассчитать относительный показатель координации.
3. На начало мая 2000г. численность граждан, состоящих на учете в службе занятости, составляла 3 064 тыс. человек, а число заявленных предприятиями вакансий – 309 тыс. Рассчитать относительный показатель интенсивности.
4. На начало 2000г. операции ГКО – ОФЗ проводили в Москве 108 официальных дилеров; в Новосибирске 16 и В Санкт – Петербурге 13. Вычислить относительный показатель сравнения.
5.Определить величину среднедушевого денежного дохода в целом по РФ.
Таблица 4.4.
Распределение населения РФ в 1 квартале 2000г. по уровню среднедушевых денежных доходов
| Среднедушевой денежный доход в среднем за месяц, тыс. руб. | Численность населения, % к итогу |
| до 400 | 30,2 |
| 400-600 | 24,4 |
| 600-800 | 16,7 |
| 800-1000 | 10,5 |
| 1000-1200 | 6,5 |
| 1200-1600 | 6,7 |
| 1600-2000 | 2,7 |
| 2000 и выше | 2,3 |
| Итого |
Литература:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 1996.-с.39-80.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Инфра – М, 2000. –с.75-106.
3. Гусаров В.М. Статистика. М.: ЮНИТА – ДАНА, 2001. –с.47-68.
4. Общая теория статистики под ред.Спирина А.А. М.: Финансы и статистика, 1996.-с.75-101.
5. Статистика: курс лекций под ред. Ионина В.Г. Изд – во НГАЭИУ, М.: Инфра – М, 1997. – с59-84.
6. Теория статистики под ред. Шмойловой Р.А. М.: Финансы и статистика, 2002. – с.151 – 174.
Тема 5. Показатели вариации и анализ частотных распределений
Понятие вариации
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по–разному сочетаются в каждом отдельном случае.
Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Дата добавления: 2016-07-22; просмотров: 4536;











