Призмы с тремя отражениями

Из призм с тремя отражениями рассмотрим две: призму Шмидта и призму Лемана.

Призма Шмидта

Призма Шмидта (рис. 2.21) дает зеркальное изображение и отклоняет оптическую ось на 45°. На вторую отражающую грань наносится отражающее покрытие.

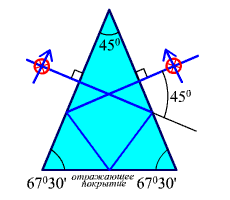
Рис. 2.21. Призма Шмидта.

Призма Лемана

Призму Лемана (рис. 2.22) можно рассматривать как комбинацию двух прямоугольных призм с углами 60° и 30°. Призма Лемана дает смещение оптической оси и зеркальное изображение. На третью отражающую грань наносится отражающее покрытие. Нерабочая часть призмы (где не проходят лучи) фрезеруется.

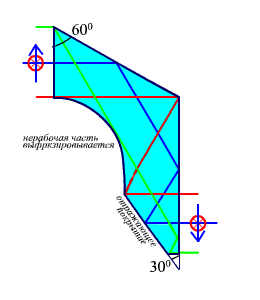
Рис. 2.22. Призма Лемана.

Расчет призм

Рассчитать призму - это не только определить ее размеры, но и определить правильное ее положение в оптической системе.

Будем рассматривать расчет призм, стоящих в непараллельных пучках лучей. В этом случае диаметры пучков лучей на входной и выходной гранях будут различными. Расчет призмы выполняется по максимальному диаметру пучка лучей.

Рассмотрим некоторые зависимости, которые используются при расчете призм.

Обратимся к рис. 2.23. Из рисунка следует, что можно найти толщину воздушной пластинки, у которой высоты луча на входной и выходной гранях будут такие же, как и у стеклянной пластинки. Следовательно, при расчетах можно заменять стеклянную пластинку на воздушную.

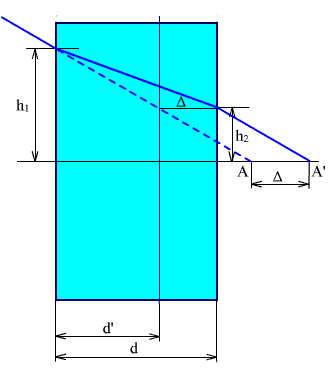
Рис. 2.23. Определение толщины редуцированной плоскопараллельной пластинки.

Воздушная пластинка d' , называется редуцированной воздушной пластинкой, у нее высоты h₁ и h₂ такие же, как и у реальной стеклянной пластинки.

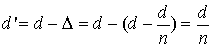
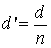- толщина редуцированной пластинки. (2.7)

Полученная формула (2.7) позволяет упростить расчеты при определении расстояний между компонентами оптической системы.

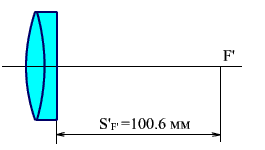
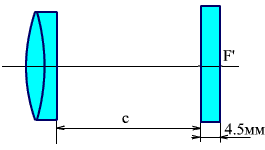
Рассмотрим пример (рис. 2.24). Пусть изображение находится в задней фокальной плоскости объектива, у которого 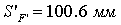. В ход лучей ввели сетку с толщиной d = 4.5 мм, показатель преломления материала сетки n = 1.5. изображение должно находиться на второй поверхности сетки. Определить расстояние между объективом и сеткой.

Рис. 2.24. Определение расстояния от объектива до сетки.

Расстояние c можно определить по формуле:

.

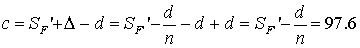Из формулы видно, что достаточно определить толщину редуцированной воздушной пластинки и отнять ее от :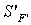

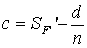(2.8)

В каждой призме существует определенная зависимость между наибольшей шириной пучка лучей, могущего пройти через призму, и длиной хода луча в призме.

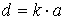, (2.9)

где d - длина хода луча в призме, k - коэффициент, характеризующий призму, a - диаметр пучка лучей, которые призма пропускает.

Для определения коэффициента k применяется развертка призмы.

Развертка призмы заключается в определении толщины плоскопараллельной пластинки, в которой длина хода луча такая же, как в исходной призме. Для нахождения развертки следует построить в последовательном порядке изображение призмы и отраженных лучей во всех отражающих гранях. На рис. 2.25 дана развертка призмы-ромб.

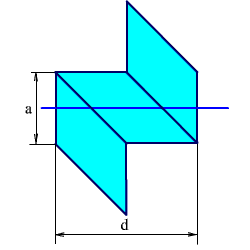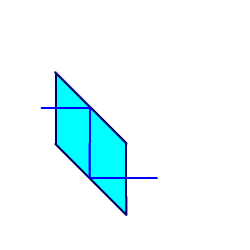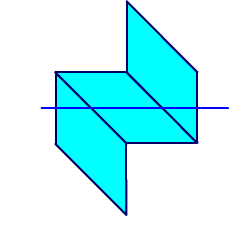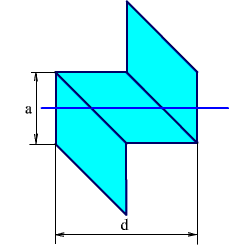
Рис. 2.25. Развертка призмы-ромб.

На рис.2.26 показано значение a и k для прямоугольных призм с одним и двумя отражениями.

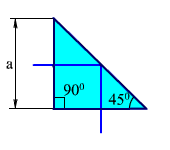k = 1

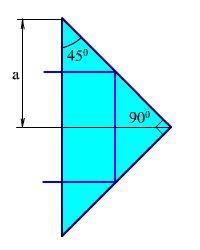k = 2

Рис. 2.26. Определение коэффициента k для прямоугольной призмы.

Определим еще одну зависимость, позволяющую выполнять расчет призм. Пусть известно положение выходной грани призмы, толщина редуцированной воздушной пластинки и положение входной грани призмы.

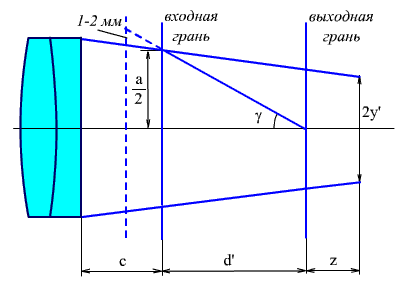
Рис. 2.27. Расчет призмы, стоящей в сходящемся пучке лучей.

Тогда из рис. 2.27 следует:

,

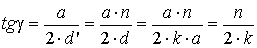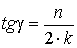. (2.10)

В формулу (2.10) не входят ни диаметр пучка a, ни длина хода луча в призме. В связи с этим может быть предложена следующая последовательность расчета призмы:

1. Проводим габаритные линии, соединяющие края объектива и края изображения.
2. Задаем положение выходной грани призмы. Если система визуальная, то .
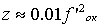3. Определяем tg γ по формуле (2.10).
4. α/2 снимаем с чертежа; чтобы не водить срезание пучков лучей размер α/2 следует увеличить на 1 - 2 мм (штриховая линия).
5. Определяем длину хода луча в призме по формуле: d = k·a .
6. Определяем толщину редуцированной пластинки: d' = d / n.
7. Определяем расстояние между объективом и призмой. Если предмет в ∞ и изображение в задней фокальной плоскости, то 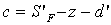. Если предмет на конечном расстоянии, тогда вместо 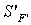используется S': 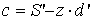. Если изображение должно находиться на второй поверхности сетки, тогда 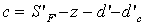, где 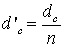, 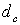- толщина сетки.

Если диаметр изображения больше диаметра объектива, тогда задается расстояние от объектива до входной грани призмы и определяется размер и положение выходной (рис. 2.28).

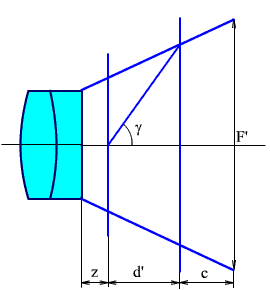
Рис. 2.28. Расчет призмы, стоящей в расходящемся пучке лучей.

Призмы с крышей

Для оборачивания изображения в плоскости, перпендикулярной плоскости чертежа, на одну из отражательных граней призмы наносят крышу: одну из отражающих граней заменяют двумя перпендикулярными друг другу плоскостями, ребро которых лежит в главном сечении призмы (рис. 2.29).

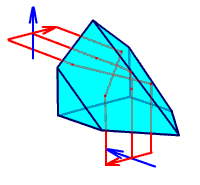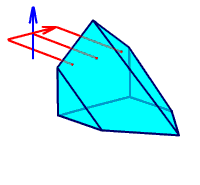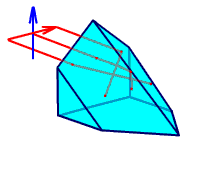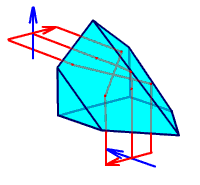
Рис. 2.29. Призма с крышей.

Лучи, идущие от горизонтальной (красной) стрелки, расположенной перпендикулярно ребру крыши, попадают, соответственно, на левую и правую отражающие поверхности крыши, затем пучки перекидываются на противоположные стороны крыши и направляются на выходную грань призмы. Происходит оборачивание стрелки справа налево.

Лучи, идущие от параллельной оси y стрелки (синей), проходят через призму с крышей так же, как и через призму без крыши.

Крышу наносят на отражающую грань, но эта грань не должна быть одновременно входной или выходной. Если одна из отражающих граней призмы требует нанесения отражающего покрытия, то крышу выгоднее наносить на эту грань, т.к. крыша не требует нанесения зеркального покрытия.

Отражающее действие призмы с крышей можно определить, используя закон отражения в векторном виде (1.9). Для этого необходимо найти выражение для ортов нормалей к граням крыши, эти нормали не лежат ни в одной из координатных плоскостей.

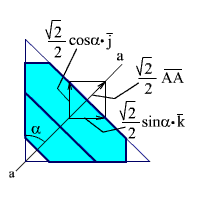
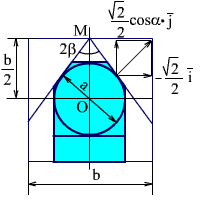
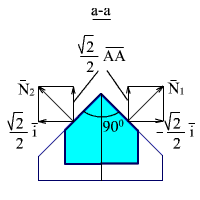
Обратимся к рис. 2.30, на котором даны сечения призмы плоскостью a - a, перпендикулярной ребру крыши (в), вид спереди (а) и вид сбоку (б). Нормали к граням крыши буду лежать в плоскости a - a. Проекции ортов нормалей на ось x и линию пересечения плоскости a - a с плоскостью xoy даны на рис. 2.30 (в). Проекция орта нормали на линию пересечения плоскостей a - a и xoy перенесена на рис. 2.30 (а) и разложена на координатные оси y и z. Угол α - угол между входной гранью и плоскостью, перпендикулярной ребру крыши.

а)

б)

в)

Рис.2.30. Призма с крышей: вид спереди, сбоку и сечение.

Выражения для ортов нормалей будут иметь вид:

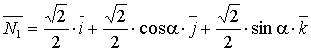
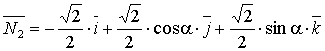
Выражения для ортов падающих лучей как в 2.1.1:

, , .

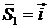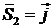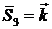Решение задачи в остальном аналогично решению, приведенному в 2.1.1, только в данном случае нужно найти отраженный луч от двух отражающих поверхностей.

Определим зависимость между диаметром пучка лучей a, который проходит через призму и размером входной грани b.

Из рис. 2.30 следует:

.

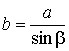Принимая во внимание:

,

,

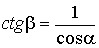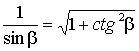получаем:

,

.

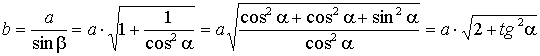Диаметр пучка лучей при прохождении через призму с крышей будет отличаться от диаметра пучка, который проходит через призму без крыши в раз.

Длина хода луча в призме с крышей равна:

,

где ,

α - угол между нормалью к ребру крыши и входной или выходной гранью.

При расчете призм с крышей по графо-аналитическому методу:

.

Все остальные расчеты выполняются так же, как и в простых призмах.

Призменные системы

Из призменных систем наиболее распространенными являются системы Малафеева первого рода (система Порро I рода) - рис. 2.31 и система Малафеева второго рода (система Порро II рода) - рис. 2.32.

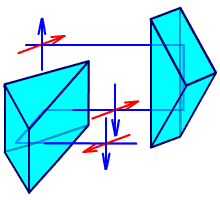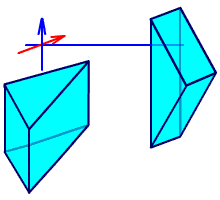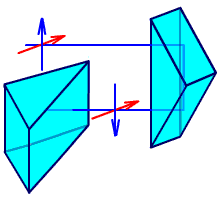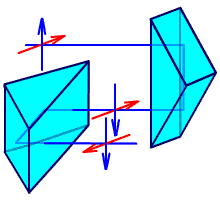
Рис. 2.31. Система Малафеева I рода.

Система Малафеева I рода состоит из двух одинаковых прямоугольных призм с двумя отражениями, главные сечения которых взаимно перпендикулярны. Такая система дает полное оборачивание.

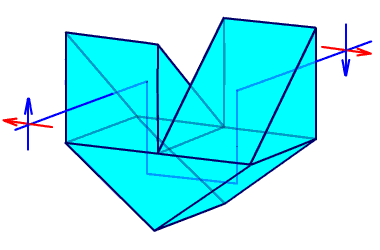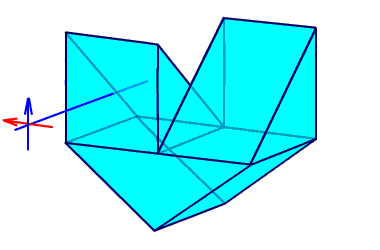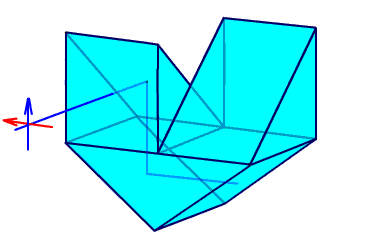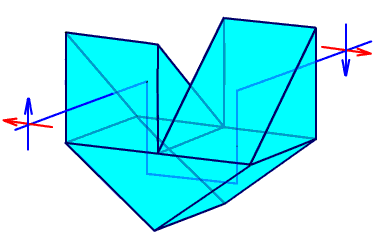
Рис. 2.32. Система Малафеева II рода.

Система Малафеева II рода состоит из двух прямоугольных призм с одним отражением и одной призмы с двумя отражениями. Эта система также дает полное оборачивание.

Клинья