Работа клиньев. Вращающиеся и перемещающиеся клинья
Клин - преломляющая призма с малым углом преломления (σ < 6°). Клинья используются в качестве компенсаторов при юстировках и измерениях.
Определим угол отклонения луча клином (рис. 2.33).
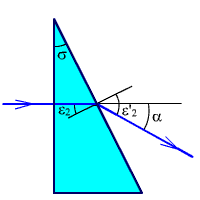
Рис. 2.33. Клин.
При малых углах закон преломления будет иметь вид:
n·ε = n'·ε.
Пусть первая поверхность перпендикулярна падающему лучу. Из рис. 2.33 следует:
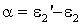 .
.
Принимая во внимание:
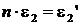 ,
,
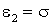 ,
,
получаем:
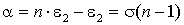 ,
,
α = σ·(n - 1). (2.11)
Угол отклонения луча клином α не меняется при повороте клина вокруг оси, перпендикулярной плоскости чертежа.
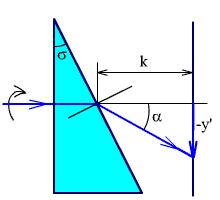
Рис. 2.34. Вращающийся клин.
Рассмотрим работу вращающихся клиньев. При вращении одного клина (рис. 2.34) изображение точки описывает окружность радиуса y'. Радиус этой окружности равен:
y' = k·α = σ·(n - 1)·k.
Для того, чтобы получить прямолинейное движение осевой точки, необходимо иметь два одинаковых вращающихся клина. На рис. 2.35 (а) показаны два клина в максимуме отклонения:
α = 2·(n - 1)·σ.
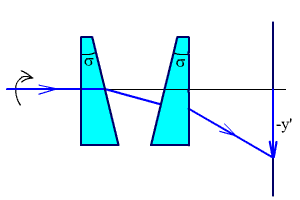 а) а)
|  б) б)
|
Рис. 2.35. Два вращающихся клина.
Если основания клиньев направлены в противоположные стороны, тогда α = 0.
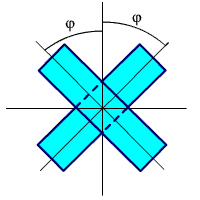
При повороте клиньев вокруг оптической оси на равные углы в противоположных направлениях (рис. 2.35 (б)), угол отклонения луча изменяется в соответствии с формулой:
α = 2·(n - 1)·σ·cos(φ).
Прямолинейное перемещение осевой точки можно получить за счет поступательного перемещения клина (рис. 2.36). В этом случае:
Δy' = z·α = z·σ(n - 1).
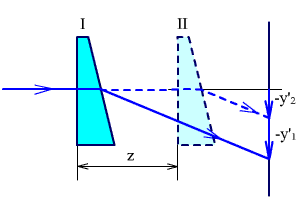
Рис. 2.36. Поступательное перемещение клина.
Поступательно перемещающийся клин для компенсации и измерения малых линейных величин является менее точным.
Вращающиеся клинья можно использовать только в параллельных пучках лучей, а перемещающиеся клинья можно использовать и в сходящихся пучках лучей.
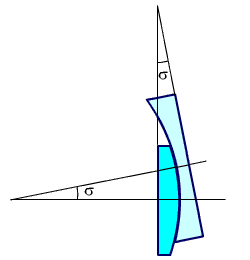
Клин с переменным преломляющим углом показан на рис. 2.37. Одна из линз перемещается относительно другой. В исходном положении две линзы вместе образуют плоскопараллельную пластинку.
| 
|
Рис. 2.37. Клин с переменным преломляющим углом.
Дата добавления: 2016-07-22; просмотров: 3410;











