Построение каркасов куба, призмы, цилиндра, конуса

Рисование каркасов геометрических тел — это передача пространственного положения, предмета на плоскости листа бумаги. Пространственное положение предмета в натуре представляет собой определенно выраженный объем, поскольку тело заполняет часть пространства. 

Вы уже знаете, что нарисовать подобие предмета или группы предметов, имеющих определенно выраженные объемы, на плоском листе бумаги невозможно без специальных знаний. Специальные знания приходят к тому, кто всерьез занялся изучением основ рисования, кто учится уметь видеть окружающий мир со всеми его предметами и явлениями.

Человека, не ознакомленного с принципами рисования, оставит равнодушным любая натурная постановка. Если ему предложить нарисовать уходящую в глубину прямую дорогу, он непременно набросает на бумаге пару сближающихся кверху, однообразных на всем протяжении от нижнего до верхнего края листа линий и не подумает даже, правильно или нет это сделано.

Итак, новое упражнение будет таким, где вам нужно передать какую-то протяженность предмета в глубину, показать его по высоте и длине (или ширине). Выходит, что предмет следует нарисовать так, чтобы в изображении он производил впечатление трехмерного (объемного). Добиться в рисунке впечатления трехмерности изображенного предмета как раз и является основной задачей рисования. Как среди всех геометрических фигур самую понятную по очертаниям форму имеет квадрат, так среди геометрических тел — куб, форма которого образуется квадратами граней, сходящимися под прямыми углами друг к другу. Ребра граней тоже сходятся у куба под прямыми углами. Если куб специально не расположить так, чтобы была видна только одна квадратная грань, все остальные его положения будут угловыми. Эти положения куба в пространстве обязательно выявят перспективные закономерности. Здесь вступает в свои права та трудность в рисовании, которую преодолевают с помощью специальных знаний о закономерностях перспективы.

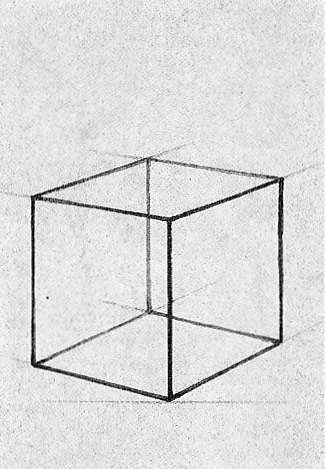
Рис. 15

Чтобы проследить данные закономерности на примере самого понятного по форме геометрического тела, выполним рисунок каркаса куба (рис. 15).

Каркас куба изготовить легко, а польза от наблюдения и анализа его формы и тем более рисования несомненна. На примере каркаса практически знакомятся с понятием «конструкция предметной формы». Следовательно, видя куб «прозрачным», «насквозь», мы воочию убеждаемся в изменениях его объема под воздействием пространственных закономерностей, т.е. перспективных сокращений. С другой стороны, каркас куба показывает нам только границы его общей формы. Заключение любого объемного тела внутри определенных границ (очертаний) со всеми присущими ему характерными признаками составляет конструктивную основу формы предмета.

Геометрические тела настолько универсальны и логичны по своей структуре, что человеческая мысль соизмерила их с математическими категориями, выведя обоснование всех объемов в ранг уникальных. Все имеющиеся на свете живые и искусственные формы представляют собой разнообразные сочетания геометрических объемов.

Итак, конструкция куба означает действительное строение формы этого геометрического тела. Именно куб по праву является первым предметом, по которому вы учитесь передавать на бумаге определенно выраженный объем.

Изображая каркас куба, вы знакомитесь с принципом строения объемной формы. Этому помогает ясное представление конструкции куба, полученное благодаря каркасу, что позволяет точнее построить изображение.

Прежде чем приступить к работе по рисованию каркаса куба, необходимо подготовить рабочее место. Затем следует выбрать точку зрения на натуру. Лучшим расстоянием до каркаса куба от рисующего будет тройной размер высоты рисуемого предмета. Натура должна быть расположена ниже уровня глаз рисующих (ниже линии горизонта) и поставлена под углом к ним.

До проведения первой легкой вертикальной линии на бумаге постарайтесь найти пропорциональные отношения величины изображения к размерам формата. Для этого надо наметить общую форму каркаса куба. Здесь надо сделать некоторое усилие — увидеть в трехмерной натуре общий плоский силуэт и нанести его абрис на лист бумага.

После того как общая форма каркаса куба намечена, можно перейти к определению конструктивной основы предмета. Такое определение начните с построения нижнего основания куба, т.е. грани, соприкасающейся с плоскостью подставки. Разумеется, грани как таковой нет, она условна, но границы в виде четырех ребер из проволоки показывают ее место. Построение основания каркаса зависит от соблюдения правил перспективы.

Далее для построения каркаса куба проведите ближайшее вертикальное ребро, высоту которого определите на глаз. От этого ребра постройте перпендикулярные ему, но подчиняющиеся правилам перспективы остальные ребра, которые хорошо видны в натуре, и завершите рисунок каркаса куба.

Рис. 16

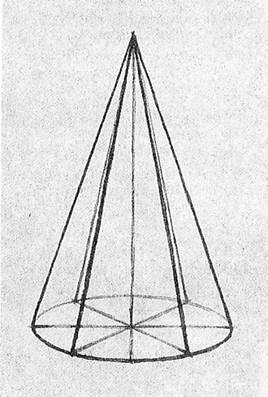
Рис. 17

Построение каркаса призмы, имеющей два основания треугольной формы, при условии, что проволочная модель расположена под углом и одна ее прямоугольная грань соприкасается с плоскостью подставки для натуры, связано с такими же способами изображения, как и в упражнении по рисованию каркаса куба. Нужно соблюсти пропорции и правила перспективы, получив, таким образом, представление о конструктивном строении еще одного геометрического тела.

Отличную возможность разобраться в принципах конструктивного построения формы дают проволочные модели еще двух геометрических тел иной формы — цилиндра и конуса. Если при рисовании куба и призмы вы встретились только с внешними границами — ребрами, образующими форму названных тел, то в новых упражнениях вы столкнетесь с принципиально новой конфигурацией натуры. Теперь в действие вступают дополнительные контуры построения — центральные оси, которые связываются с круглыми основаниями, а последние — друг с другом с помощью нескольких образующих (рис. 16, 17).

Но самым характерным в рисовании каркасов цилиндра и конуса будет изменение формы оснований, зрительно превращающихся из круглых в овальные (эллипсовидные). Проявите необходимое внимание к проволочным моделям, доведите каждый рисунок до полного сходства с натурой.

Контрольные вопросы

1. Что надо понимать под конструктивной основой формы?

2. Как объяснить конструктивную основу формы куба?

3. Что следует понимать под простыми и сложными формами?

4. Что такое пропорции предмета?

5. Как вы понимаете «золотую пропорцию»?

6. Как построить перспективу окружности?

7. Что вы понимаете под большой формой?