Корреляционной функции между входом и выходом
Преобразовав уравнение (4) к матричной форме и выделяя вектор импульсной функции w(t), получим следующее соотношение
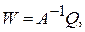 (5)
(5)
где выражения для отдельных матиц имеют вид
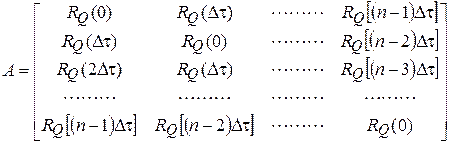 , (6)
, (6)
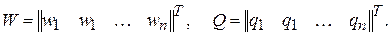 (7)
(7)
где элементы qi=RQq(iDt)/Dt – вычисляются через ординаты взаимной корреляционной функции, wi – ординаты импульсной функции, RQ(i) – значения корреляционной функции входа.
Следует отметить, что для получения решения в виде вектора значений импульсной функции в среде Delphi7.0 применяются алгоритмы для численного решения систем алгебраических уравнений либо матричных вычислений, что требует написания соответствующих алгоритмов. В среде MATLAB данная процедура не вызывает затруднений, поскольку имеются специализированные математические функции.
Ниже представлен пример, реализующий такое решение:
A=toeplitz(Ruu);
w=inv(A)*Ryu';
где Ruu – вектор автокорреляционной функции, Ryu – вектор взаимной корреляционной функции. Функция T = toeplitz(С) возвращает симметрическую матрицу Теплица, определяемую однозначно вектором С.
Первая строка реализует встроенную функцию составления матрицы Теплица, с помощью которой получается матрица A, определяемая выражением (6). Вторая строка примера реализует вычисление вектора w по формуле (5), который содержит значения импульсной функции. На рис. 3, а - изображена полученная в результате вычислений, импульсная функция.
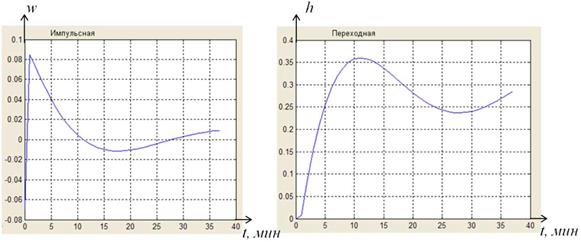
А б
Рис. 3. График импульсной функции и переходной функции
Определяя переходную функцию как интеграл от импульсной функции получаем кривую, изображенную на рис.3, б. Для вычисления интеграла в MATLAB имеется возможность численного интегрирования, например, используя функцию интегрирования методом трапеций. Ниже представлен пример вычисления переходной функции
for i=2:1:tm-2;
k=1:1:i;
f(i)=trapz(t(k),w(k));
end;
где tm - длинна вектора импульсной функции (w), f - получаемый вектор переходной функции; trapz(X,Y) - возвращает интеграл от функции Y по переменной X, используя метод трапеций (пределы интегрирования в этом случае задаются начальным и конечным элементами вектора X).
Внешний вид временных характеристик на рис.3, характеризующих динамику объекта, показывает, что передаточная функция объекта имеет вид колебательного звена, далее следует найти постоянные времени и коэффициент усиления.
Для удобства ввода исходных данных и получения графиков было разработано приложение в расширении среды MATLAB – GUI (Graphical User Interfaces), которое позволяет разрабатывать свои приложения с возможностью использования функций среды MATLAB.
Приложение (рис.4) содержит кнопки загрузки входного и выходного сигналов, компоненты задания интервалов данных из файлов с возможностью прореживания, графики входного и выходного сигнала, флажки выбора метода расчета корреляционных функций (с аппроксимацией или без) компоненты задания степени полинома аппроксимации корреляционных функций, графики корреляционной и взаимной корреляционной функции и графики импульсной и переходной функций, а также другие компоненты применяемые для настройки расчетов.
Загрузка сигналов в MATLAB производится с использованием процедуры мастера выбора текстового файла uigetfile, процедур открытия файла fopen и чтения строк fgetl. Ниже представлен пример загрузки данных в приложение.
[FileName, PathName] = uigetfile('*.txt;');
FullName = [PathName FileName];
FT = fopen(FullName,'r'); for i=1:1:max_len
VF = fgetl(FT); u1(i) = str2double(VF); end;
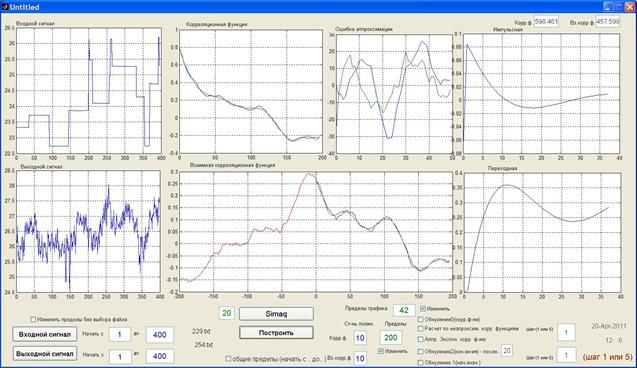
Рис. 4. Приложение в среде MATLAB с применением GUI
Таким образом, можно сказать, что пакет MATLAB предоставляет все необходимые средства для решения задач идентификации по статистическим данным.
Использование при разработке приложения расширения GUI (Graphical User Interfaces) облегчает решение сложных математических задач, позволяет разрабатывать свои приложения, делать их независимыми (возможность работы без требования установки среды MATLAB), дополнять инструментами ввода и вывода информации и вместе с тем пользоваться всей мощью представленных библиотек математических функций.
Список литературы
1. Порхало В.А., Рубанов В.Г. Получение математической модели обжига клинкера на основе решения уравнения Винера-Хопфа. // Сб. трудов XXIII Междун. науч. конф. «Математические методы в технике и технологиях» (ММТТ-23). ― Саратов: СГТУ, 2010. ― Т.10. ― С. 132―135.
2. Дьяконов В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений: специальный справочник. Спб.: Питер, 2002. 608 с.
АНАЛИЗ ИССЛЕДОВАНИЙ В ОБЛАСТИ СОВЕРШЕНСТВОВАНИЯ ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ ПРОИЗВОДСТВА И РЕМОНТА ПОДВИЖНОГО СОСТАВА
Анализируя все многообразие причин, обеспечивающих в той или иной степени, условия безопасности движения поездов, мы пришли к выводу, что, наряду с традиционными причинами (надежность подвижного состава, условия эксплуатации, технический и психологический уровень персонала и т.п.), существенное влияние, на безопасность движения поездов, оказывает также уровень и качество технической подготовки производства предприятий (рис. 1), производящих капитальные ремонты (КР) подвижного состава [1].
Традиционно известно, что технологическая подготовка производства (ТПП) представляет собой совокупность взаимосвязанных процессов, обеспечивающих технологическую готовность предприятия к выпуску изделий заданного уровня качества при установленных сроках, объеме выпуска и затратах.
Исследования, направленные на совершенствование технологической подготовки производства на предприятиях по ремонту подвижного состава являются наименее изученным, но не менее важным аспектом организации ремонтного производства.
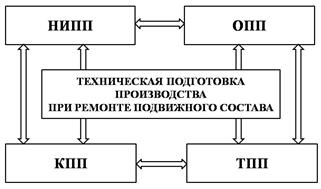
Рис. 1. Структурная схема технической подготовки производства по ремонту подвижного состава [3]:
Дата добавления: 2020-10-14; просмотров: 592;











