ПРИМЕНЕНИЕ СРЕДЫ MATLAB И РАСШИРЕНИЯ GUI ДЛЯ ИДЕНТИФИКАЦИИ СЛОЖНОГО ОБЪЕКТА

Решение задач статистического анализа случайных процессов, с целью идентификации сложных объектов, возможно с применением большого числа математических пакетов. Специализированные пакеты обычно реализуют методы, используемые в конкретной предметной области. Анализ статистических данных требует от математического пакета наличия необходимых функций, удобного интерфейса настройки параметров вычислений, вывод графических результатов. Ниже рассмотрено применение известной среды MATLAB для получения математической модели процесса обжига клинкера.

Для решения задачи получения математической модели по статистическим данным во временной области воспользуемся уравнением Винера-Хопфа:

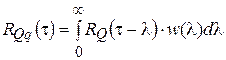, (1)

где корреляционную функцию R_Q(τ) входа и взаимную корреляционную функцию R_Qq(τ) между входом и выходом определяют по измеряемым входному Q(τ) и выходному q(τ) сигналу объекта. Решая данное уравнение можно найти импульсную переходную (весовую) функцию w(t), а по ней и передаточную функцию W(s).

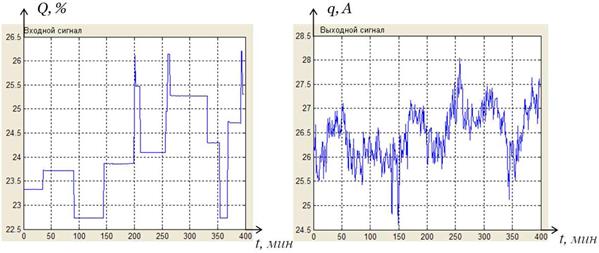
В процессе управления цементной печью используют большое количество измеряемых и управляемых сигналов, на рис.1. представлены графики: а - степень открытия шибера дымососа, б - нагрузка на главном приводе двигателя печи. Ниже рассмотрено получение весовой функции, характеризующей взаимосвязь между этими сигналами.

А б

Рис. 1. Графики изменения входного и выходного параметров

Цементной печи

В [1] изложено решение задачи идентификации на основе решения уравнения Винера-Хопфа с применением среды Delphi7.0, в которой было разработано программное приложение. При этом для вычисления оценок корреляционных функций составляется алгоритм, реализующий следующие соотношения

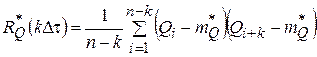, (2)

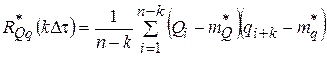, (3)

где Q_i=Q[i], q_i=q[i] – значения случайного сигнала в i-ом сечении; m_Q^* и m_q^* – оценки мат. ожиданий; R_Q^* и R_Qq^* – оценки корреляционной и взаимокорреляционной функций случайных процессов.

Программная среда Delphi 7.0 является хорошим средством написания объектно-ориентированных программ и программ, связанных с различными базами данных, но не обладает необходимыми для наших целей библиотеками математических функций, и для целей математического моделирования гораздо удобнее использовать специализированные математические пакеты, такие как MathCAD или MATLAB.

С целью унификации программного средства для получения математической частной модели процесса обжига клинкера была разработана программа в среде MATLAB, которая позволяет получать корреляционные функции, взаимные корреляционные функции исследуемых сигналов, весовые функции, переходные функции. Для оценки точности вычислений с использованием предложенного инструментария было произведено сравнение найденных графиков с расчетами, полученными в среде MathCAD. Проверка показала хорошее совпадение получаемых расчетных данных и графиков.

Стоит отметить, что определение корреляционных функций в MATLAB производится гораздо проще, чем в среде программирования Delphi7.0, поскольку в перовй для этого существует специальная математическая функция xcorr, которую можно использовать в расчетах.

Функция вычисления взаимной корреляции векторов и матриц хсоrr имеет несколько форм записи [2], которые представлены ниже:

С=хсоrr (А,В) - для векторов А и В с длиной М > 1 возвращает оценку взаимной корреляции в виде вектора С длиной 2М – 1 (в ином случае возвращает 0);

xcorr(A) при векторе А возвращает оценку автокорреляции;

хсоrr (.. ,SCALE0PT) - задает способ масштабирования корреляционной функции. Значение SCALE0PT определеяет следующие вычисления:

'biased' - вычисляется смещенная оценка корреляционной функции как 1/М;

'unbiased' - вычисляется несмещенная оценка корреляционной функции как 1/(M-abs(lags));

'coeff' - осуществляется масштабирование так, чтобы значение корреляционной функции при нулевом смещении было равно 1,0;

'none' - масштабирование не производится (задано по умолчанию).

Применение функции хсоrr иллюстрирует следующий пример:

ryu=xcorr(y2,u2,'biased');

ryu3=ryu(n:n+tm-2);

где y2, u2 - векторы, содержащие значения выходного и входного сигнала соответственно, n - размер векторов.

После применения функции хсоrr второй строкой выделяется область положительных значений, поскольку функция возвращает вектор значений корреляционной функции от –n до n. На рис.2. показаны графики вычисленных с использованием данной функции корреляционной функции входа и взаимной корреляционной функции между входом и выходом.

Как видно корреляционные функции удовлетворяют требованиям эргодических стационарных процессов и стремятся с течением времени к нулю.

Решая интегральное уравнение Винера-Хопфа (1) численными методами, его сводят к решению системы алгебраических уравнений с числом уравнений равным количеству полученных ординат корреляционных функций (2) - (3). При этом интеграл в уравнении (1) представляется конечной суммой:

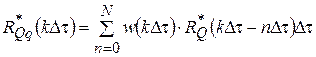. (4)

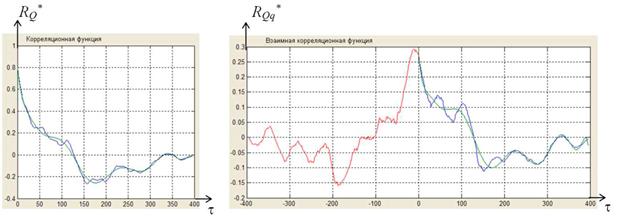
А б

Рис. 2. Оценки: а - корреляционной функции входа, б - взаимной