Методы определения коэффициента Хилла

Существуют два метода определения коэффициента Хилла: метод, предложенный самим Хиллом и метод, разработанный Кургановым Б.И. с соавторами. В первом случае уравнение Хилла логарифмируется и преобразуется, приобретая следующий вид

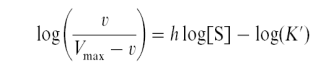
Это уравнение используют для построения графика, из которого можно определить величину h. График строится в координатах lоgv/(V_MAX – v) против lg[S].

Пример линеаризованного графика Хилла приведен на рис. 2.4.5. Степень сигмоидности на линейных участках позволяет выявить силу кооперативности между центрами в олигомерном ферменте.

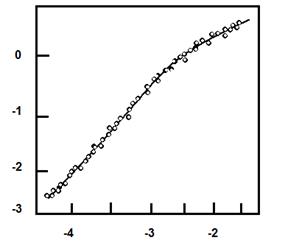
Рис. 2.4.5. Линеаризованная сигмоидная зависимость

Определение коэффициента Хилла по логарифмической зависимости требует знания V_max. Однако не всегда эта величина известна.

Курганов Б.И. с соавт. предложили так называемый разностный метод определения коэффициента Хилла. В этом случае строится график в координатах 1/v от log [S] (рис. 2.4.6).

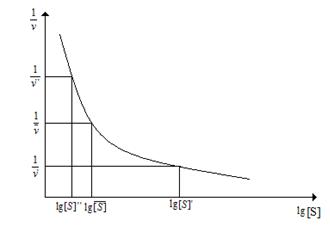
Рис. 2.4.6. Определение коэффициента Хилла «разностным» методом

Для нахождения коэффициента Хилла на кривой 1/v от log [S] выбираются три точки с координатами {1/v′;log [S]′}, {1/v; log [S]} и {1/v′′; log [S]′′}. Значения [S] для крайних точек отличаются отличаются от значений [S] для средней точки на постоянный множитель, обозначаемый ϰ (ϰ> 1): [S]′= [S]/ϰ и [S]′′=[S]ϰ.

Коэффициент Хилла рассчитывают далее по формуле:

h= log{(1/v′ - 1/v)/ (1/v - 1/v′′)}/ logχ

Суть этих преобразований сводится к следующему:

Разности обратных величин уже не содержа параметра V_max , а отношение разностей при определенном выборе значений 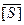; [S]ʹ; [S]ʹʹ - не содержит как параметра V_max и [S]_0,5.

Поэтому этот способ определения коэффициента Хилла получил название разносного метода.

После нахождения параметра коэффициента Хилла, остальные два параметра V_max и [S]_0,5 могут быть определены путем представления экспериментальных данных в координатах 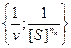(рис. 2.4.7) в соответствии со следующим линейным соотношением.

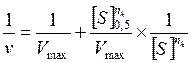
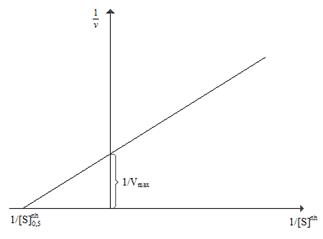
Рис. 2.4.7. Линеаризация уравнения Хилла с учетом величины коэффициента Хилла в координатах Лайнуивера-Берка

Коэффициент Хилла является параметром уравнения Хилла и не имеет физического смысла. Однако при достаточно сильных взаимодействиях коэффициент Хилла близок n (число активных центров в молекуле фермента). Таким образом, h ≤ n.

Оценить кооперативные взаимодействия в молекуле аллостерического фермента возможно с помощью коэффициента крутизны – R_х, предложенного Кошландом.

[S]_0,9

R_x = ------- , где

[S]_0,1

[S]_0,9 – концентрация субстрата, при которой достигается 0,9 от V_MAX;

[S]_0,1 ‒ концентрация субстрата, при которой достигается 0,1 от V_MAX.

Концентрации субстратов, при которых достигается 0,1 и 0,9 от максимальной скорости реакции можно определить, построив график зависимости скорости реакции от концентрации субстрата. Найдя по графику максимальную скорость, рассчитываем 0,1V_MAX и 0,9V_MAX и, опустив перпендикуляр на ось абсцисс, находим величины [S]_0,1 и [S]_0,9.

Для ферментов, подчиняющихся кинетике Михаэлиса-Ментен, коэффициент крутизны равен 81. Ферменты, характеризующиеся положительной кооперативностью, имеют коэффициент крутизны меньше 81, а отрицательной кооперативностью – больше 81.

Между коэффициентом Хилла и коэффициентом крутизны существует определенная зависимость:

R_x = 81^1/h,

В случае, когда h=1, уравнение Хилла превращается в уравнение Михаэлиса-Ментен.

Отношение [S]_0,9/[S]_0,1, индекс кооперативности, является обратной мерой кооперативных взаимодействий. Другими словами, большая разность в концентрации субстрата требуется для перехода от v=0,1Vmax до v=0,9Vmax, большие величины [S]_0,9/[S]_0,1 свидетельствуют о слабой степени кооперативности между центрами.

Так как коэффициент Хилла и индекс кооперативности (коэффициент крутизны) для олигомерных ферментов связаны друг с другом, вместе они позволяют измерить степень кооперативности между связывающими центрами и минимальное число этих взаимодействий. В случае гомотропных взаимодействий для молекул субстрата график зависимости v от [S] является сигмоидной кривой.

Это отражает ситуацию, когда с ферментом связываются несколько молекул субстрата, при этом связывание первой молекулы некоторым образом ускоряет связывание второй молекулы, т.е. при связывании с ферментом более чем одной молекулы субстрата наблюдается кооперативный эффект.

Такое поведение системы предполагает, что существует пороговая концентрация субстрата, ниже которой изменение его концентрации оказывает относительно небольшое влияние на скорость ферментативной реакции, однако при превышении порога даже небольшие изменения концентрации субстрата оказывают значительное влияние. Следовательно, в пределах относительно узкой области концентрации субстрата скорость ферментативной реакции изменяется очень резко, что весьма важно для аллостерических ферментов, поскольку многие из них являются регуляторными.

Для доказательства аллостерической природы положительной кооперативности по субстрату можно использовать прием десенсибилизации фермента. Для этого можно осуществить кратковременное его нагревание. Например, десенсибилизацию аспартаткарбамоилтрансферазы Герхард и Парди осуществляли в течение четырех минут при 60^◦С, а УДФ-глюкозо-4-эпимераза в течение двух минут при 41^◦С. Десенсибилизация может быть вызвана другими физическими воздействиями или химическим модифицированием фермента. Шанжё одним из первых добился десенсибилизации треониндегидротазs из E.coli по отношению к аллостерическому ингибитору – L-изолейцину при помощи n-хлормеркурийбензоата. Для десенсибилизации аллостерических ферментов (фосфофруктокиназы, глутаматдегидрогеназы и аспартаткиназы) осуществляли облучением растворов ферментов рентгеновскими лучами. После десенсибилизации ферменты не теряли каталитическую активность и утрачивали возможность регулироваться аллостерическими эффекторами.