Методы расчета ЭДУ.

Расчет ЭДУ ведется либо на основании закона взаимодействия проводника с током и магнитным полем (1-й метод) 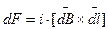, либо по изменению запаса магнитной энергии системы (2-й метод).

1-й метод. Возьмем систему из двух произвольно расположенных проводников 1 и 2, обтекаемых токами i₁ и i₂ (рис. 32). Напряженность магнитного поля, создаваемого элементом dy проводника 2 в месте расположения элемента dx проводника 1, будет равна

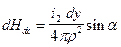, (71)

где 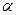- угол между вектором 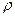и направлением тока по элементу dy. Весь проводник 2 создает в месте расположения элемента dx напряженность магнитного поля, равную

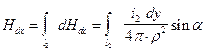. (72)

Учитывая, что 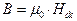, элементарная сила, действующая на элемент dx, обтекаемый током i₁, будет Рис. 32. К расчету ЭДУ равна:

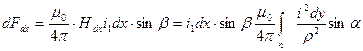, (73)

где 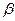– угол между вектором магнитной индукции В и вектором тока i₁; 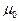– магнитная проницаемость воздуха.

Полную силу взаимодействия между проводниками 1 и 2 получим после интегрирования (76) по всей длине проводника 1,

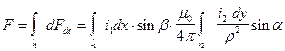. (74)

Считая токи i₁ и i₂ неизменными по всей длине проводников последнее уравнение можно переписать в виде произведения

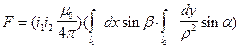. (75)

Первый член этого выражения зависит только от значений токов. Второй член зависит только от взаимного геометрического расположения проводников и представляет собой безразмерную величину. Эту величину часто называют коэффициентом контура и обозначают буквой С.

Тогда сила взаимодействия будет равна 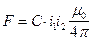. (76)

Учитывая, что 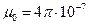Г/м, то тогда

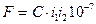, (77)

то-есть, сила взаимодействия между проводниками, обтекаемыми токами i₁ и i₂ пропорциональна произведению этих токов и зависит от геометрии проводников и их взаимного расположения.

2-й метод. Электромагнитное поле вокруг проводников и контуров с током обладает определенным запасом энергии. Электромагнитная энергия контура, обтекаемого током i равна

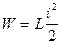. (78)

Электромагнитная энергия двух контуров, обтекаемых токами i₁ и i₂

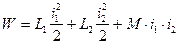, (79)

где L₁ и L₂ – индуктивности контуров; M – взаимная индуктивность контуров.

Всякая деформация контура или изменение взаиморасположения контуров приводит к изменению запаса магнитной энергии. При этом работа сил в любой системе равна изменению запаса электромагнитной энергии этой системы.

Fdx = dW . (80)

Здесь dW – изменение запаса магнитной энергии системы при деформации в направлении x под действием силы F.

На этом законе и основан второй метод определения ЭДУ в контурах. ЭДУ в контуре или между контурами, действующее в направлении x , равно скорости изменения запаса энергии системы при деформации ее в том же направлении

F_x = dW/dx . (81)

Согласно этому, ЭДУ в контуре, обтекаемом током, будет равно

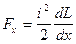, (82)

где dx – деформация контура по радиусу (если dx = 0, то и dL = 0).

ЭДУ между двумя взаимосвязанными контурами с токами i₁ и i₂ будет равно

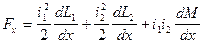. (83)