Методы решения размерных цепей

В зависимости от того, какие параметры заданы, а какие является неизвестными, существует два вида решаемых с использованием размерных цепей задач- проектные(прямые) и проверочные(обратные).

Проектная задача состоит в том, чтобы по заданным параметрам замыкающего звена определить параметры составляющих звеньев.

Проверочная задача состоит в том, чтобы по известным параметрам составляющих и замыкающих звеньев определить (проверить) значения замыкающих звеньев.

В практике машиностроения используются два метода решения размерных цепей: метод полной взаимозаменяемости (расчёт на максимум- минимум) и теоретико-вероятностный.

Метод полной взаимозаменяемости предполагает, что размеры принимают крайние, т.е. максимальные или минимальные значения. Формула расчёта по этому методу имеет вид:

для допусков 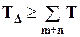; для погрешностей .

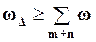До определения операционных размеров необходимо для каждой размерной цепи, в которой замыкающим размером является конструкторский размер, проверить и обеспечить выполнение условия

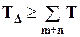(1)

Для этого ещё неизвестные составляющие размеры определяются приближенно, по номиналам рабочего чертежа, а допуски на них назначаются в соответствии с экономической точностью той операции, в которой они выполняются.

В случае если соотношение (1) не выполняется, приходится назначать более жесткие допуски на составляющие звенья в сравнении с рекомендуемыми (ужесточать допуски). Затем при решении размерных цепей используются только эти ужесточенные допуски.

Достоинства метода: простота, отсутствие брака, отсутствие необходимости знать законы вероятностного распределения составляющих звеньев.

Недостатки: расчёт базируется на предположении, что все размеры входят в цепь с предельными значениями; вероятность этого мала.

Теоретико-вероятностный метод -предполагает, что размеры составляющих и замыкающих звеньев могут изменяться случайным образом.

Допуск замыкающего звена по этому методу определяется по формуле:

,

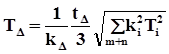где k_Δ , k_i - коэффициенты относительного рассеяния замыкающего и составляющего звеньев. Они характеризуют степень отличия распределения погрешностей размеров от закона нормального распределения. Коэффициент k_iпринимают: k_i =1,0- для закона нормального распределения; k_i =1,22 - для закона Симпсона; k_i =1,73 - для закона равной вероятности;

t_Δ - коэффициент, выбираемый в зависимости от процента риска. При риске Р = 0,27% t_Δ = 3,0.

Коэффициент относительного рассеяния замыкающего звена k_Δопределяется по формуле П.Ф.Дунаева.

Достоинства метода: учитывает реальную картину при конструировании и изготовлении изделий; позволяет значительно расширить допуски на составляющие звенья.

Недостатки: необходимо знать законы вероятностного распределения составляющих звеньев; громоздкие формулы для расчёта коэффициентов; вероятность появления брака.