Метод кривых распределения

Используется как в массовом, так и в серийном производствах. Метод заключается в следующем: из партии обработанных заготовок выбирается группа, проводятся замеры геометрических параметров, и выполняется статистический анализ. При статистическом анализе необходимо соблюдать следующие условия:

1. Для анализа берут детали, обработанные одним режущим инструментом или между двумя подналадками станка.

2. Измерение проводят измерительным инструментом с ценой деления не превышающей (1/6…1/10)Т.

3. Число деталей, взятых для статистического анализа должно быть достаточно большим (желательно 50 и более, но не меньше 20 деталей).

Рассмотрим алгоритм определения суммарной погрешности обработки:

1. Производится обработка парии N деталей на настроенном оборудовании в автоматическом цикле.

2. Выполняется замер анализируемого геометрического параметра.

3. Строится практическая кривая распределения. Для этого определяются:

- размах варьирования: R = A_max - A_min;

- число интервалов К, которое зависит от размеров партии (при N£50 … 100 шт., К=5…7);

- размер интервала С= R / К;

- частота попадания размеров в каждый интервал n_i;

- координаты середины интервалов А_срi.

- строится практическая кривая распределения (рисунок 26).

4. Строится теоретическая кривая распределения (в большинстве случае это кривая Гаусса). Её построение выполняют в следующем порядке:

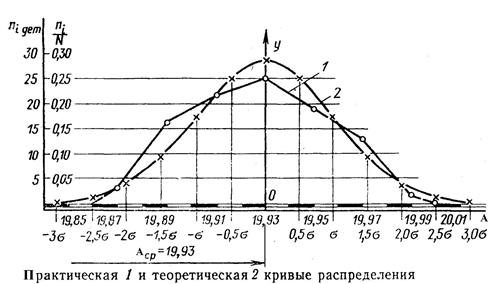
Рисунок 26 – Кривые распределения

- определяется координата центра группирования размеров (средний размер) и среднее квадратичное отклонение по формулам:

, ;

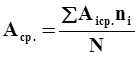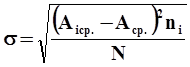- определяются координаты у для характерных точек кривой Гаусса ±s, ±2s, ±3s;

- строится кривая Гаусса .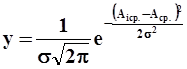

5. Определяется суммарная погрешность. Для этого определяются:

-погрешность от случайных и закономерно изменяющихся факторов

Δ_р. =6s;

- постоянная погрешность, вызванная неточностью настройки станка,

Δ_н. =|А_ср. – А_Тср.| ;

- суммарная погрешность Δ_å = 2Δ_н. + Δ_р.

Возможны следующие случаи расположения кривой относительно поля допуска:

1. Δ_å< Т, Δ_н. =0 - обработка обеспечивает заданное качество;

2. Δ_å< Т, Δ_н. ≠ 0- требуется поднастройка станка;

3. Δ_å> Т,- возможно появление брака. Брак может быть не исправимый и исправимый.

Метод имеет следующий недостаток: полученная погрешность характеризует точность законченного процесса, а влияние случайных и закономерно изменяющихся факторов оценивается совместно, что не даёт возможности прогнозировать изменение точности в процессе дальнейшей обработки.

Раздельно определить влияние на точность случайных и закономерно изменяющихся погрешностей позволяет метод точностных диаграмм.