Тема 2.4. Информация в непрерывных сигналах

Обобщим теперь понятия энтропии и взаимной информации на ансамбли непрерывных сигналов. Пусть 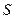- случайная величина (сечение или отсчёт случайного сигнала), определённая в некоторой непрерывной области, и её распределение вероятностей характеризуется плотностью .

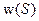Разобьём область значений 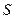на небольшие интервалы протяжённостью 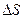. Вероятность того, что 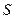лежит в интервале 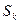, 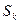+ 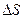, то есть 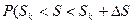, приблизительно равна 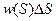, причём приближение тем точнее, чем меньше интервал 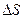. Степень неожиданности такого события равна 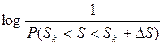. Если значения 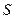в пределах конечного интервала 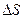заменить значениями 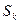в начале интервала, то непрерывный ансамбль заменится дискретным, а его энтропия определится как:

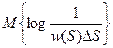
Будем теперь увеличивать точность определения значения 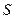, уменьшая интервал 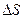. В пределе, при должна получиться энтропия непрерывной случайной величины:

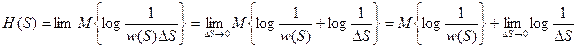
(2.19)

Второй член в полученном выражении стремится к 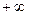и совершенно не зависит от распределения вероятностей 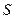. Это значение , что собственная информация любой непрерывной случайной величины бесконечно велика. Тем не менее, взаимная информация между двумя непрерывными ансамблями, как правило, остаётся конечной. Такова будет, в частности, взаимная информация между переданным и принятым сигналами, так что по каналу связи информация передаётся с конечной скоростью.

Обратим внимание на первый член в данной формуле. Он является конечным и определяется плотностью распределения вероятности 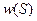. Его называют дифференциальной энтропией и обозначают :

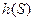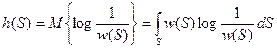(2.20)

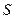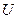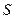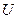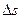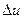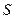Попытаемся теперь определить взаимную информацию между двумя непрерывными случайными величинами и . Разбив области определения и соответственно на небольшие интервалы и , заменим эти непрерывные величины дискретными так же, как это делалось при выводе формулы . Исходя из этого выражения можно определить взаимную информацию между непрерывными величинами и :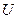

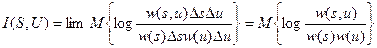(2.21)

При этом никаких явных бесконечностей не появилось, и действительно, в обычных случаях взаимная информация оказывается конечной. С помощью простых преобразований её можно представить и в таком виде:

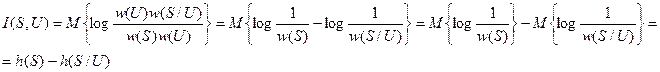
(2.22)

Здесь 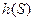- определённая ранее дифференциальная энтропия 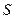, а 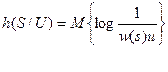- условная дифференциальная энтропия. Легко убедиться, что основные свойства взаимной информации остаются справедливыми и в данном случае.

В качестве примера найдём дифференциальную энтропию случайной величины 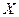с нормальным распределением вероятности:

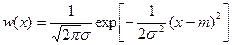, (2.23)

где 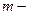математическое ожидание, а 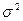- дисперсия .

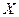Подставив (2.23) в (2.20), найдём:

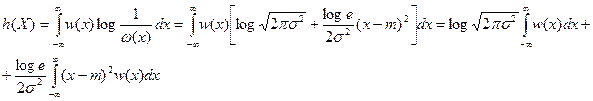
Первый интеграл по общему свойству плотности вероятности равен 1, а второй – по определению дисперсии равен 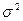. Окончательно

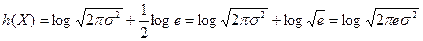(2.24)

Таким образом, диффиринциал энтропия гауссовский случайной величины не зависит от её математического ожидания и монотонно возрастает с увеличением дисперсии.

В заключение укажем одно важное свойство нормального распределения: из всех непрерывных случайных величин 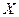с одинаковой дисперсией 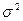наибольшую дифференциальную энтропию имеет величина с нормальным распределением.