Эффективное кодирование дискретных сообщений

Применим полученные результаты к проблеме кодирования дискретных сообщений. Пусть 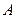- источник последовательности элементарных сообщений (знаков) с объёмом алфавита 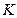и производительностью 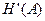. Для передачи по дискретному каналу нужно преобразовать сообщения в последовательность кодовых сигналов 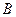так, чтобы эту кодовую последовательность можно было затем однозначно декодировать. Для этого необходимо, чтобы скорость передачи информации от источника к кодеру 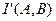равнялась производительности источника 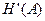, 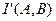= 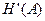. Но с другой стороны из предыдущего: 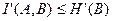. Следовательно, необходимым условием для кодирования является 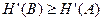или, обозначая через 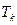длительность кодового символа, через 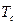длительность элементарного сообщения, 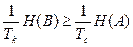, или

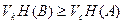, (2.17)

где 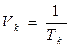- число кодовых символов, a 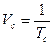- число сообщений, передаваемых в секунду.

Будем рассматривать для простоты только двоичный код, при котором алфавит 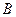состоит из символов 0 и 1. Тогда 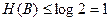бит. Поэтому, необходимое условие сводится к тому, что:

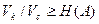(2.18)

Но это отношение представляет среднее число кодовых символов, приходящихся на одно элементарное сообщение. Таким образом, для возможности кодирования и однозначного декодирования сообщения необходимо, чтобы среднее число двоичных символов на сообщение было не меньше энтропии 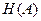. Является ли это условие достаточным?

Одна из основных теорем теории информации утверждает, что оно “почти достаточно”. Точнее, содержание теоремы кодирования для источника заключается в том, что передавая двоичные символы со скоростью 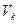симв/с можно закодировать сообщения так, чтобы передавать их со скоростью:

(сообщений в секунду),

где 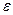- сколь угодно малая величина.

Эта теорема почти тривиальна, если источник передаёт сообщения независимо и равновероятно. В этом случае 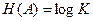и, если ещё к тому же 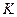-целая степень двух 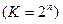, то .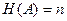

Таким образом можно закодировать сообщения любого источника с объёмом алфавита 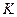, затрачивая 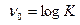двоичных символов на элементарное сообщение. Если, однако, сообщения передаются не равновероятно, и (или) не независимо, то 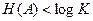и возможно более экономное кодирование с затратой 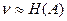символов на сообщение. Относительная экономия символов при этом окажется равной 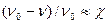. Таким образом, избыточность определяет достижимую степень ”сжатия сообщения”.

Рассмотрим несколько примеров.

Так, если элементарными сообщениями являются русские буквы 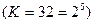и они передаются равновероятно и независимо, то 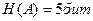. Каждую букву можно закодировать последовательностью из пяти двоичных символов, поскольку существует 32 такие последовательности.

Разумеется, таким же равномерным кодом можно закодировать и буквы в связном русском тексте, и именно так часто поступают на практике. Но можно обойтись значительно меньшим числом символов на букву. Для русского литературного текста 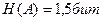и, следовательно, возможен способ эффективного кодирования (или кодирования со сжатием сообщения), при котором в среднем на букву русского текста будет затрачено немногим более 1,5 двоичных символа, то есть на 70% меньше, чем при примитивном коде.

Существует довольно много способов сжатия сообщений или сокращения избыточности текста. Так, например:”Эта фр. напис. сокращ. и тем не м. мож. надеят., что Вы пойм. её прав.” В предыдущей фразе удалось уменьшить число букв, а следовательно и символов, если её кодировать равномерным кодом почти на 40%.

Другая возможность заключается в том, чтобы кодировать не отдельные буквы, а целые слова.

Дальнейшее сжатие сообщений возможно путём применения неравномерного кода, если более короткие последовательности используются для более частых букв (слов) и более длинные – для более редких. Заметим, что эта идея неравномерного кодирования впервые нашла применение в телеграфном коде Морзе, в котором наиболее короткие комбинации использованы для часто встречающихся букв (е, и, т, с, а).

Применение неравномерного кода позволяет снизить избыточность, вызванную неравной вероятностью между сообщениями.

Разработано много методов эффективного кодирования для различных источников. Задача эффективного кодирования наиболее актуальна не для передачи текста, а для других источников со значительно большей избыточностью. К ним относятся, например, телевизионные передачи (промышленное телевидение), некоторые телеметрические системы, в которых возможно сжатие в десятки раз, фототелеграфия.