Алфавитное кодирование, порядок его применения.

Пусть А={a1,a2,a3,…,an} – алфавит.

a1, a2, a3, …, an – элементы алфавита, т.е. буквы.

Тогда последовательность букв – слово. Множество слов – выражение.

Если α = a1, a2, … ak – то к – длина слова.

Если α = a1, a2 , то a1 называется префиксом (или началом) слова, а a2 – постфиксом (концом) слова.

Алфавитное кодирование задается схемой (или таблицей кодов) σ:

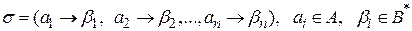
Пример:

А = {0,1,2,3,4,5,6,7,8,9}

B = {0,1}

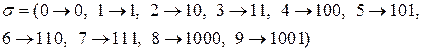
Эта схема однозначна, но кодирование не является взаимно однозначным: 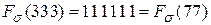, а значит невозможно декодирование.

Однако если добавить по одному символу, то каждый символ будет кодироваться тетрадами. Такая схема позволяет однозначное кодирование.

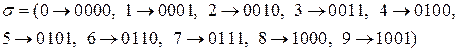
Схема алфавитного кодирования называется разделимой, если любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование.

Схема называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы.

Например.

А = {a,b}

B = {0,1}

σ = {a -> 0; b -> 01} данная схема разделима. Но не префиксна. Следовательно, свойство быть префиксной буквой достаточное, но не необходимое для разделимости кода. Хотя префиксная схема всегда является разделимой.

Для получения разделимой схемы алфавитного кодирования необходимо чтобы длины элементарных кодов удовлетворяли соотношению, известному как неравенство Макмиллана.

Если числа длиной L1, L2, … , Ln соответствуют длинам элементарных кодов β1, β2, …, βn и удовлетворяют: ∑ (i от 1 до n) (2 в степени –Li) меньше либо равно 1, то существует схема σ <α1 ->β1; α2 -> β2; … αn -> βn>

Пример.

Схему кодирования, лежащую в основе азбуки Морзе, можно записать

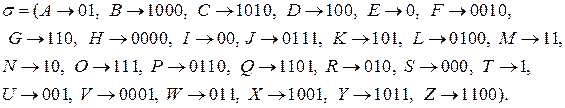
по историческим и техническим причинам 0 называется точкой, а 1 – тире. Проведя проверку на разделимость получим

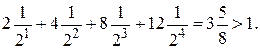
Таким образом, схема азбуки Морзе не является разделимой. На самом деле, в азбуке Морзе используются дополнительные элементы – паузы между буквами и словами, что позволяет декодировать сообщение.