Двоичное кодирование
Одиночный цифровой сигнал не слишком информативен, ведь он может принимать только два значения: нуль и единица. Поэтому в тех случаях, когда необходимо передавать, обрабатывать или хранить большие объемы информации, обычно применяют несколько параллельных цифровых сигналов. При этом все эти сигналы должны рассматриваться только одновременно, каждый из них по отдельности не имеет смысла. В таких случаях говорят о двоичных кодах, то есть о кодах, образованных цифровыми (логическими, двоичными) сигналами. Каждый из логических сигналов, входящих в код, называется разрядом. Чем больше разрядов входит в код, тем больше значений может принимать данный код.
В отличие от привычного для нас десятичного кодирования чисел, то есть кода с основанием десять, при двоичном кодировании в основании кода лежит число два (рис. 2.9). То есть каждая цифра кода (каждый разряд) двоичного кода может принимать не десять значений (как в десятичном коде: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а всего лишь два — 0 и 1. Система позиционной записи остается такой же, то есть справа пишется самый младший разряд, а слева — самый старший. Но если в десятичной системе вес каждого следующего разряда больше веса предыдущего в десять раз, то в двоичной системе (при двоичном кодировании) — в два раза. Каждый разряд двоичного кода называется бит (от английского "Binary Digit" — "двоичное число").
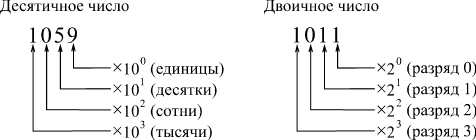
Рис. 2.9. Десятичное и двоичное кодирование
В табл. 2.3 показано соответствие первых двадцати чисел в десятичной и двоичной системах.
Из таблицы видно, что требуемое количество разрядов двоичного кода значительно больше, чем требуемое количество разрядов десятичного кода. Максимально возможное число при количестве разрядов, равном трем, составляет при десятичной системе 999, а при двоичной — всего лишь 7 (то есть 111 в двоичном коде). В общем случае n-разрядное двоичное число может принимать 2n различных значений, а n-разрядное десятичное число — 10n значений. То есть запись больших двоичных чисел (с количеством разрядов больше десяти) становится не слишком удобной.
| Таблица 2.3. Соответствие чисел в десятичной и двоичной системах | |||
| Десятичная система | Двоичная система | Десятичная система | Двоичная система |
Для того чтобы упростить запись двоичных чисел, была предложена так называемая шестнадцатеричная система (16-ричное кодирование). В этом случае все двоичные разряды разбиваются на группы по четыре разряда (начиная с младшего), а затем уже каждая группа кодируется одним символом. Каждая такая группа называется полубайтом (или нибблом, тетрадой), а две группы (8 разрядов) — байтом. Из табл. 2.3 видно, что 4-разрядное двоичное число может принимать 16 разных значений (от 0 до 15). Поэтому требуемое число символов для шестнадцатиричного кода тоже равно 16, откуда и происходит название кода. В качестве первых 10 символов берутся цифры от 0 до 9, а затем используются 6 начальных заглавных букв латинского алфавита: A, B, C, D, E, F.

Рис. 2.10. Двоичная и 16-ричная запись числа
В табл. 2.4 приведены примеры 16-ричного кодирования первых 20 чисел (в скобках приведены двоичные числа), а на рис. 2.10 показан пример записи двоичного числа в 16-ричном виде. Для обозначения 16-ричного кодирования иногда применяют букву "h" или "H" (от английского Hexadecimal) в конце числа, например, запись A17F h обозначает 16-ричное число A17F. Здесь А1 представляет собой старший байт числа, а 7F — младший байт числа. Все число (в нашем случае — двухбайтовое) называется словом.
| Таблица 2.4. 16-ричная система кодирования | |||
| Десятичная система | 16-ричная система | Десятичная система | 16-ричная система |
| 0 (0) | A (1010) | ||
| 1(1) | B (1011) | ||
| 2 (10) | C (1100) | ||
| 3 (11) | D (1101) | ||
| 4 (100) | E (1110) | ||
| 5 (101) | F (1111) | ||
| 6 (110) | 10 (10000) | ||
| 7 (111) | 11 (10001) | ||
| 8 (1000) | 12 (10010) | ||
| 9 (1001) | 13 (10011) |
Для перевода 16-ричного числа в десятичное необходимо умножить значение младшего (нулевого) разряда на единицу, значение следующего (первого) разряда на 16, второго разряда на 256 (162) и т.д., а затем сложить все произведения. Например, возьмем число A17F:
A17F=F*160 + 7*161 + 1*162 + A*163 = 15*1 + 7*16+1*256+10*4096=41343Но каждому специалисту по цифровой аппаратуре (разработчику, оператору, ремонтнику, программисту и т.д.) необходимо научиться так же свободно обращаться с 16-ричной и двоичной системами, как и с обычной десятичной, чтобы никаких переводов из системы в систему не требовалось.
Помимо рассмотренных кодов, существует также и так называемое двоично-десятичное представление чисел. Как и в 16-ричном коде, в двоично-десятичном коде каждому разряду кода соответствует четыре двоичных разряда, однако каждая группа из четырех двоичных разрядов может принимать не шестнадцать, а только десять значений, кодируемых символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. То есть одному десятичному разряду соответствует четыре двоичных. В результате получается, что написание чисел в двоично-десятичном коде ничем не отличается от написания в обычном десятичном коде (табл. 2.6), но в реальности это всего лишь специальный двоичный код, каждый разряд которого может принимать только два значения: 0 и 1. Двоично-десятичный код иногда очень удобен для организации десятичных цифровых индикаторов и табло.
| Таблица 2.6. Двоично-десятичная система кодирования | |||
| Десятичная система | Двоично-десятичная система | Десятичная система | Двоично-десятичная система |
| 0 (0) | 10 (1000) | ||
| 1(1) | 11 (1001) | ||
| 2 (10) | 12 (10010) | ||
| 3 (11) | 13 (10011) | ||
| 4 (100) | 14 (10100) | ||
| 5 (101) | 15 (10101) | ||
| 6 (110) | 16 (10110) | ||
| 7 (111) | 17 (10111) | ||
| 8 (1000) | 18 (11000) | ||
| 9 (1001) | 19 (11001) |
В двоичном коде над числами можно проделывать любые арифметические операции: сложение, вычитание, умножение, деление.
Рассмотрим, например, сложение двух 4-разрядных двоичных чисел. Пусть надо сложить число 0111 (десятичное 7) и 1011 (десятичное 11). Сложение этих чисел не сложнее, чем в десятичном представлении:
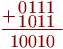
При сложении 0 и 0 получаем 0, при сложении 1 и 0 получаем 1, при сложении 1 и 1 получаем 0 и перенос в следующий разряд 1. Результат — 10010 (десятичное 18). При сложении любых двух n-разрядных двоичных чисел может получиться n-разрядное или (n+1)-разрядное число.
Точно так же производится вычитание. Пусть из числа 10010 (18) надо вычесть число 0111 (7). Записываем числа с выравниванием по младшему разряду и вычитаем точно так же, как в случае десятичной системы:
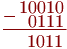
При вычитании 0 из 0 получаем 0, при вычитании 0 из 1 получаем 1, при вычитании 1 из 1 получаем 0, при вычитании 1 из 0 получаем 1 и заем 1 в следующем разряде. Результат — 1011 (десятичное 11).
При вычитании возможно получение отрицательных чисел, поэтому необходимо использовать двоичное представление отрицательных чисел.
Для одновременного представления как двоичных положительных, так и двоичных отрицательных чисел чаще всего используется так называемый дополнительный код. Отрицательные числа в этом коде выражаются таким числом, которое, будучи сложено с положительным числом такой же величины, даст в результате нуль. Для того чтобы получить отрицательное число, надо поменять все биты такого же положительного числа на противоположные (0 на 1, 1 на 0) и прибавить к результату 1. Например, запишем число –5. Число 5 в двоичном коде выглядит 0101. Заменяем биты на противоположные: 1010 и прибавляем единицу: 1011. Суммируем результат с исходным числом: 1011 + 0101 = 0000 (перенос в пятый разряд игнорируем).
Отрицательные числа в дополнительном коде отличаются от положительных значением старшего разряда: единица в старшем разряде определяет отрицательное число, а нуль — положительное.
Помимо стандартных арифметических операций, в двоичной системе счисления используются и некоторые специфические операции, например, сложение по модулю 2. Эта операция (обозначается A) является побитовой, то есть никаких переносов из разряда в разряд и заемов в старших разрядах здесь не существует. Правила сложения по модулю 2 следующие: 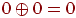 ,
, 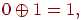
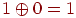 ,
,  . Эта же операция называется функцией Исключающее ИЛИ. Например, просуммируем по модулю 2 два двоичных числа 0111 и 1011:
. Эта же операция называется функцией Исключающее ИЛИ. Например, просуммируем по модулю 2 два двоичных числа 0111 и 1011:
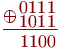
Среди других побитовых операций над двоичными числами можно отметить функцию И и функцию ИЛИ. Функция И дает в результате единицу только тогда, когда в соответствующих битах двух исходных чисел обе единицы, в противном случае результат —0. Функция ИЛИ дает в результате единицу тогда, когда хотя бы один из соответствующих битов исходных чисел равен 1, в противном случае результат 0.
Дата добавления: 2017-06-13; просмотров: 6449;











