Тема 4.3 Кванторные операции над предикатами.
Специфическая природа предикатов, позволяет ввести над ними такие операции, которые не имеют аналогов среди операций над высказываниями. Имеются в виду две кванторные операции над предикатами.
1. Квантор общности
Для превращения одноместного предиката в высказывание нужно вместо его переменной подставить какой-нибудь конкретный предмет из области задания предиката. Имеется еще один способ для такого превращения – это применение к предикату операций связывания квантором общности или квантором существования. Каждая из этих операций ставит в соответствие одноместному предикату некоторое высказывание, истинное или ложное в зависимости от исходного предиката.
Операцией связывания квантором общности называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве М, сопоставляется высказывание, обозначаемое 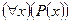 , которое истинно в том и только в том случае, когда предикат Р(х) тождественно истинен, и ложно в противном случае, то есть
, которое истинно в том и только в том случае, когда предикат Р(х) тождественно истинен, и ложно в противном случае, то есть
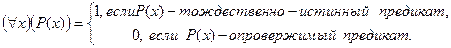
Словесным аналогом квантору общности " является: «для любого», «для каждого», «для всякого» и т.п.
В выражении 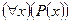 переменная х уже перестает быть переменной в обычном смысле этого слова, то есть вместо нее невозможно подставить какие бы то ни было конкретные значения. Говорят, что переменная х связанная.
переменная х уже перестает быть переменной в обычном смысле этого слова, то есть вместо нее невозможно подставить какие бы то ни было конкретные значения. Говорят, что переменная х связанная.
Если одноместный предикат Р(х) задан на конечном множестве М = {a1, a2, …, an}, то высказывание 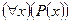 эквивалентно конъюнкции Р(а1)Ù Р(а2)Ù … Ù Р(аn).
эквивалентно конъюнкции Р(а1)Ù Р(а2)Ù … Ù Р(аn).
Пример. Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы 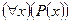 .
.
Решение. Выражение 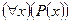 означает «все люди смертны». Оно не зависит от переменной х, а характеризует всех людей в целом, т. е. выражает суждение относительно всех х множества М.
означает «все люди смертны». Оно не зависит от переменной х, а характеризует всех людей в целом, т. е. выражает суждение относительно всех х множества М.
Операцией связывания квантором общности по переменной х1 называется правило, по которому каждому n-местному (n ³ 2) предикату Р(х1, х2, …, хn), определенному на множествах М1, М2, …, Мn, сопоставляется новый (n-1)-местный предикат, обозначаемый 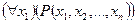 , который для любых предметов
, который для любых предметов 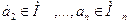 , превращается в высказывание
, превращается в высказывание 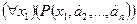 , истинное в том и только в том случае, когда одноместный предикат
, истинное в том и только в том случае, когда одноместный предикат 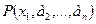 , определенный на множестве М1, тождественно истинен, и ложное в противном случае, то есть:
, определенный на множестве М1, тождественно истинен, и ложное в противном случае, то есть:
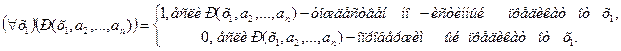
Дата добавления: 2016-07-22; просмотров: 2328;











