Практическое занятие 2. Приближенное решение уравнения пьезопроводности при условии постоянного дебита скважины. Расчеты P(r,t)

Теоретическая часть

Решение уравнения пьезопроводности необходимо при расчетах изменений пластовых давлений в процессе эксплуатации нефтяной скважины в нефтяном пласте, а также при расчетах изменения давлений в водоносном пласте и на контуре газовой или нефтяной залежи, эксплуатируемой как укрупненная скважина.

Дифференциальное уравнение, называется уравнением пьезопроводности, и имеет вид в декартовых координатах:

æ 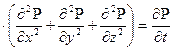(1.1)

или для неустановившегося плоско-радиального течения:

æ 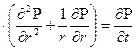. (1.2)

Получено решение этого уравнения в предложении, что пласт неограничен и введен сток (скважина) с постоянным дебитом Q.

P₀ - начальное давление в невозмущенном пласте

t₀=момент пуска стока

P(r,t) – давление в точке «r» пласта, в момент времени t от мгновения пуска скважины.

Основная формула упругого режима:

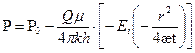(1.3)

Интегральная показательная функция:

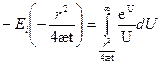(1.4)

Таблица 1.1 – Значения интегральной показательной функции, х=r²/4ǽt

х		10-4	10-2	0.1				∞
-Ei(-x)	∞	8.631	4.04	1.82	0.22	0.049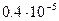

Основная формула упругого режима записывается в безразмерном виде, где х=r²/4ǽt

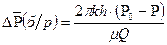; (1.4)

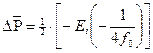
Залежь рассматривается как укрупненная скважина, пущенная в бесконечном водоносном пласте, тогда основная формула дает падение давления на контуре залежи газа R_з при постоянном дебите воды, вторгающейся в залежь.

Задача 1. Определить давление работающей залежи с дебитом воды Q в произвольной точке водоносного пласта в различных моментах времени.

Исходные данные: Q=10³ м³/сут; P_нач.=100атм.; к=1 дарси; β^*=10^-41/атм; h=10м; µ=0,01 Па сек.

æ = 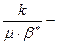назван Щелкачевым коэффициентом пьезопроводности

Найдем длину радиуса

R =70 n = 70 * 19 = 1330 м n – номер варианта, для примера n=19.

Найдем величину коэффициента: :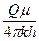

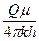=9,2 атм

Далее: æ = = 8640 м²/сут.

Находим значения t и P для данных таблицы 1.1 t=r²/4ǽx

P вычисляется из формулы 1.3

Полученные результаты записываем в виде таблицы.

Таблица 2.1 – Результаты расчетов

х		10-4	10-2	0.1				∞
-Ei(-x)	∞	8/631	4.04	1.82	0.22	0.049
ti, сут	∞			511,8	51,18	25,59	5,118
Рi, атм	-∞	20,6	62,832	83,256	97,976	99,55	99,999996

Варианты расчетов определяются по значениям: n=1,2,3……. и т. д.

Практическое занятие 3. Параметры укрупненной модели нефтяного пласта. Определение упругого запаса. Расчеты добычи нефти и объемов внедрения воды по заданной динамике падения среднего давления

Теоретическая часть

Основные параметры теории упругого режима. Коэффициент объемной упругости жидкости и пласта.

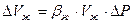(2.1)

Коэффициент объемной упругости воды 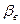изменяется в зависимости от давления, температуры, количества растворенного газа. В некоторых диапазонах 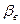можно считать постоянным.

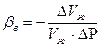(2.2)

,

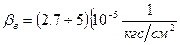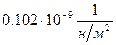
Пласт считается однородной упругой средой, подчиняющейся закону Гука. Относительное изменение порового объема пласта пропорционально изменению давления. Скелет породы испытывает давление

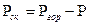(2.3)

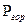- горное давление, 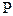- давление флюида, считая горное давление постоянным.

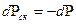
Сжимаемость скелета 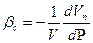, здесь V- выделенный объем пласта, V_п - поровый объем.

Упругий запас выделенной области пласта определяется как количество жидкости, высвобождающейся из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет упругого расширения жидкости и скелета породы.

Пример.

Пласт объемом V=10⁹м³ (1км³)

,

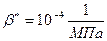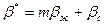
Начальное давление 16 МПа,

Давление насыщения 6 МПа,

Залежь нефти замкнута

Вопрос: сколько можно добыть нефти до давления насыщения:

упругий запас ,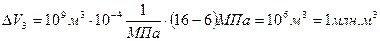

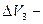упругий запас при снижении давления на 10 МПа

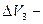упругий запас =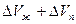

,

,

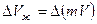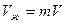
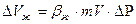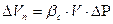
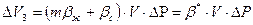
Коэффициент упругоемкости пласта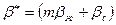

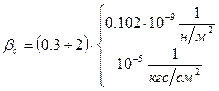
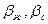имеют одинаковые порядки.

Если пласт замкнутый, эксплуатируется при упругом режиме, то добыча нефти за период падения, средневзвешенного давления Р₀ - 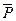составит упругий запас

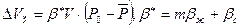
C другой стороны, отобрано жидкости за время t:

q·t

Уравнение баланса: q·t = .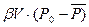

Если рассматривать малый период "dt", взять дифференциал баланса:

,

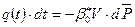получим дифференциальное уравнение: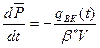

Рассмотрим нефтяную залежь, окруженную водным бассейном. Законтурную область плоскорадиальной фильтрации воды от удаленного контура R_∞ до контура нефтеносности залежи R_к представим как замкнутую. Тогда для неё аналогичное уравнение материального баланса, как для замкнутого контура нефтяной залежи:

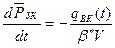
здесь 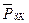- средневзвешенное давление законтурной области;

q_ВК (t) – расход воды в нефтяную залежь.

Приняв приближенно фильтрацию воды в водном бассейне стационарной по Дюпюи:

,

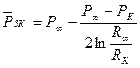получим:

,

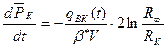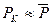
Пусть нефтяная залежь эксплуатируется при водонапорном режиме с притоком воды через контур нефтеносности. Тогда исходный баланс:

q·t = .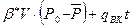

Так, упругий баланс составит:

.

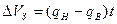Дифференциальное уравнение материального баланса:

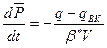
В этом случае падение давления меньше, чем для замкнутого пласта.

Задача 1. Определить объемы добычи нефти Q_доб.н. и объемы внедрения воды Q_в. Из решения системы интегральных уравнений:

P(t) – P_нач. = – (Q_доб.н – Q_в.)/β_нV_н (2.4)

P(t) – P_нач. = – (Q_в. 2 ln(R_k/R_ус))/ β_вV_в (2.5)

Уравнения 1, 2 решают на различных шагах снижения давления. Варианты:

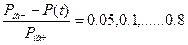
Система решается как система двух линейных алгебраических уравнений с двумя неизвестными.

Исходные данные: V_н= 10⁸ м³, V_в= 10⁹ м³, β_н=10^-41/атм, β_в=10^-51/атм, P_нач.=100 атм, R_k/R_ус=10, ln(R_k/R_ус)= 2,3;