Сравнение качественных признаков
Критерий χ2
Условия применения: объем выборки n 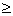 40, выборочные данные сгруппированы в интервальный вариационный ряд с числом интервалов не менее 7, ожидаемые (теоретические) частоты интервалов не должны быть меньше 5.
40, выборочные данные сгруппированы в интервальный вариационный ряд с числом интервалов не менее 7, ожидаемые (теоретические) частоты интервалов не должны быть меньше 5.
Проверяемая гипотеза H0 состоит в том, что плотность распределения генеральной совокупности, из которой была взята выборка соответствует теоретической модели.
Хи-квадрат = ∑(Э - Т)² / Т
df = (R - 1) * (C - 1), где R – количество строк в таблице, C – количество столбцов.
К примеру, психолог хочет узнать, действительно ли то, что учителя более предвзято относятся к мальчикам, чем к девочкам. Т.е. более склонны хвалить девочек. Для этого психологом были проанализированы характеристики учеников, написанные учителями. Данные о частоте встречаемости слов были занесены в таблицу:
| «Активный» | «Старательный» | «Дисциплинированный» | |
| Мальчики | |||
| Девочки |
Для этого построим таблицу распределения эмпирических частот, т.е. тех частот, которые мы наблюдаем:
| «Активный» | «Старательный» | «Дисциплинированный» | Итого: | |
| Мальчики | ||||
| Девочки | ||||
| Итого: | n = 48 |
Теоретически, мы ожидаем, что частоты распределятся равновероятно, т.е. частота распределится пропорционально между мальчиками и девочками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую суму (n).
| «Активный» | «Старательный» | «Дисциплинированный» | Итого: | |
| Мальчики | (21 * 16)/48 = 7 | (21 * 17)/48 = 7.44 | (21 * 15)/48 = 6.56 | |
| Девочки | (27 * 16)/48 = 9 | (27 * 17)/48 = 9.56 | (27 * 15)/48 = 8.44 | |
| Итого: | n = 48 |
Итоговая таблица для вычислений будет выглядеть так:
| Категория 1 | Категория 2 | Эмпирич. | Теоретич. | (Э-Т)2/Т |
| Мальчики | «Активный» | 1,28 | ||
| «Старательный» | 7,44 | 0,8 | ||
| «Дисциплини-рованный» | 6,56 | 0,47 | ||
| Девочки | «Активный» | |||
| «Старательный» | 9,56 | 0,62 | ||
| «Дисциплини-рованный» | 8,44 | 0,04 | ||
| Сумма: 4,21 |
В нашем случае хи-квадрат = 4,21; df = 2.
По таблице критических значений критерия находим: при df = 2 и уровне ошибки 0,05 критическое значение χ2 = 5,99.
Полученное значение меньше критического, а значит принимается нулевая гипотеза. Вывод: учителя не придают значение полу ребенка при написании ему характеристики.
Сравнение долей
Для сравнения частот применяется Т-критерий Стьюдента для долей
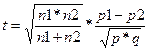
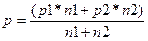
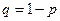
Точный тест Фишера
Точный метод Фишера—Ирвина (критерий Фишера—Ирвина, точный метод Фишера) применяется для проверки нулевой гипотезы о том, отобраны ли две исследуемые бинарные (дихотомические) выборки из генеральных совокупностей с одинаковой частотой встречаемости изучаемого эффекта. Рассматриваемый метод предназначен для обработки так называемых четырехпольных (четырехклеточных) таблиц, или таблиц «2 х 2».
Таблицы 2х2 или четырехпольные таблицы имеют вид
| Есть эффект | Нет эффекта | ||
| 1 группа | a | b | a+b |
| 2 группа | c | d | c+d |
| a+c | b+d | a+b+c+d |
где a,b,c,d - наблюдаемые частоты
a+b, c+d - суммы частот по строкам
a+c, b+d - суммы частот по колонкам
a+b+c+d - общее число наблюдений
В результате вычислений получается точное значение уровня значимости нулевой гипотезы. Вычисление производится по формуле:
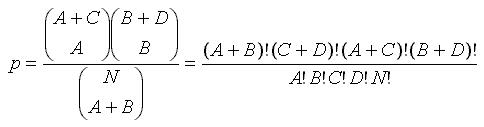
Допустим имеется таблица "2х2" следующего вида:
Подсчитываем маргинальные частоты для данной таблицы:
p=(2+3)!*(6+4)!*(2+6)!*(3+4)!/((2+3+6+4)!*2!*3!*6!*4!)=0,326
Для вычисления одностороннего значения уровня значимости необходимо найти сумму всех вероятностей для комбинаций данной таблицы со значениями от 0 до вероятности данной таблицы (0,326).
Для вычисления двустороннего значения уровня значимости необходимо найти сумму всех вероятностей для комбинаций данной таблицы со значениями меньше или равными данной таблицы (0,326).
Минимальная маргинальная частота равна 5, поэтому для данной таблицы возможно (5+1) комбинаций с заданными маргинальными частотами.
| p=(0+5)!*(8+2)!*(0+8)!*(5+2)!/((0+8+5+2)!*0!*8!*5!*2!)=0,007 | ||
| p=(1+4)!*(7+7)!*(1+7)!*(4+7)!/((1+4+7+7)!*1!*4!*7!*7!)=0,093 | ||
| p=(2+3)!*(6+4)!*(2+6)!*(3+4)!/((2+3+6+4)!*2!*3!*6!*4!)=0,326 | ||
| p=(3+2)!*(5+5)!*(3+5)!*(2+5)!/((3+2+5+5)!*3!*2!*5!*5!)=0,392 | ||
| p=(4+1)!*(4+6)!*(4+4)!*(1+6)!/((4+1+4+6)!*4!*1!*4!*6!)=0,163 | ||
| p=(5+0)!*(3+7)!*(5+3)!*(0+7)!/((5+0+3+7)!*5!*0!*3!*7!)=0,019 | ||
Таким образом уровень значимости для односторонней гипотезы составляет:
P=0,326 +0,093 + 0,007 = 0,426
а для двусторонней гипотезы:
P=0,326 + 0,093 + 0,007 + 0,163 + 0,019 = 0,608
Дата добавления: 2020-10-01; просмотров: 700;











