Парный критерий Т – Вилкоксона
Для решения задач, в которых осуществляется сравнение двух рядов чисел психолог может использовать парный критерий Т - Вилкоксона. Этот критерий применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, т. е. он позволяет установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом.
Критерий Т основан на ранжировании абсолютных величин разности между двумя рядами выборочных значений в первом и втором эксперименте (например, до и после какого-либо воздействия). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем наряду с общей суммой рангов находится отдельно сумма рангов, как для положительных, так и для отрицательных сдвигов. Если интенсивность сдвига в одном направлении оказывается большей, то и соответствующая сумма рангов также оказывается больше. Этот сдвиг называется типичным, а противоположный, меньший по сумме рангов сдвиг - нетипичным. Эти два сдвига оказываются дополнительными друг другу. Критерий Т - Вилкоксона базируется на величине нетипичного сдвига, который называется Тэмп.
Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений.
Для решения этой задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В таблице приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т - Вилкоксона.
| До | После | Сдвиг | Абсолютные величины разностей | Ранги | Нетипичный сдвиг | |
| -2 | 10,5 | |||||
| -1 | 6,5 | |||||
| 6,5 | * | |||||
| -8 | ||||||
| -11 | ||||||
| -20 | ||||||
| -18 | ||||||
| -1 | 6,5 | |||||
| 6,5 | * | |||||
| -22 | ||||||
| -1 | 6,5 | |||||
| -2 | 10,5 | |||||
| -6 | 13,5 | |||||
| -4 | ||||||
| -1 | 6,5 | |||||
| 13,5 | * | |||||
| Сумма | 26,5 |
Обработка данных по критерию Т - Вилкоксона осуществляется следующим образом:
В четвертый столбец таблицы вносятся величины сдвигов с учетом знака. Их вычисляют путем вычитания из чисел третьего столбца соответствующих чисел второго столбца.
В пятом столбце в соответствие каждому значению сдвига ставят его абсолютную величину.
В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце.
По формуле: подсчитывают сумму рангов. В нашем примере она составляет:
12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + 10,5 + 13,5 + 12 + 6,5 + 13,5 +2 = 190
Проверяют правильность ранжирования на основе совпадения сумм рангов полученных двумя способами. В нашем случаи обе величины совпали, 190 = 190, следовательно, ранжирование проведено правильно.
Любым символом отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае это три положительных сдвига.
Суммируют ранги нетипичных сдвигов. Это и будет искомая величина . В нашем случае эта сумма равна: = 6,5 + 13,5 + 6,5 = 26,5.
Ткрит для P<=0,05=53
Ткрит для P<=0,01=38
Cледовательно, можно утверждать, что зафиксированные в эксперименте изменения не случайны и значимы на 1% уровне. Таким образом, психолог может говорить о том, что применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы, следовательно, оказывает положительное влияние на развитие внимания школьников.
Критерий X2r Фридмана
Назначение критерия
Критерий X2r применяется для сопоставления показателей, измеренных в трех или более условиях на одной и той же выборке испытуемых.
Критерий позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений.
Данный критерий является распространением критерия Т Вилкоксона на большее, чем 2, количество условий измерения. Однако здесь мы ранжируем не абсолютные величины сдвигов, а сами индивидуальные значения, полученные данным испытуемым в 1, 2, 3 и т. д. замерах.
Гипотезы
Н0: Между показателями, полученными (измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в разных условиях, существуют неслучайные различия.
Например, если у испытуемого в первом замере определена скорость прохождения графического лабиринта 54 сек, во втором замере - 42 сек, а в третьем замере - 63 сек, то эти показатели получат ранги, соответственно, 2, 1, 3, поскольку меньшему значению, полученному во втором замере, мы начислим ранг 1, среднему значению, полученному в первом замере - ранг 2, а наибольшему значению, полученному в третьем замере - ранг 3.
После того, как все значения будут проранжированы, подсчитываются суммы рангов по столбцам для каждого из произведенных замеров.
Если различия между значениями признака, полученными в разных условиях, случайны, то суммы рангов по разным условиям будут приблизительно равны. Но если значения признака изменяются в разных условиях каким-то закономерным образом, то в одних условиях будут преобладать высокие ранги, а в других - низкие. Суммы рангов будут достоверно различаться между собой. Эмпирическое значение критерия X2r и указывает на то, насколько различаются суммы рангов. Чем больше эмпирическое значение X2r ,тем более существенные расхождения сумм рангов оно отражает.
Если X2rравняется критическому значению или превышает его, различия статистически достоверны.
Тест Мак-Немара
Критерий Мак-Немара - является аналогом параметрического критерия Стьюдента и непараметрического критерия Вилкоксона, применяется для анализа связанных измерений в случае изменения реакции с помощью дихотомической переменной.
| До | После | |
| a | b | |
| c | d |
Этот метод позволяет сравнить долю респондентов, которые не имели некоторой характеристики (0) во время первого обследования (например до воздействия), но стали обладать ею во время повторного обследования (1), с долей тех, кто имел это свойство (1), но перестал иметь его после (0).
Вычисляются два значения хи-квадрат: для ячеек А и D и для ячеек B и C. A/D хи-квадрат проверяет гипотезу о том, что частоты в ячейках A и D (верхняя левая, нижняя правая) одинаковы. B/C хи-квадрат проверяет гипотезу о равенстве частот в ячейках B и C (верхняя правая, нижняя левая). Метод не может использоваться для выборок, содержащих меньше 10 элементов.
Для ячеек А и D эмпирическое значение хи-квадрат для теста Мак-Немара вычисляется по формуле
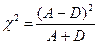
Нулевая гипотеза формулируется как Н0: P(A) = P(D).
Для ячеек B и C эмпирическое значение хи-квадрат для теста Мак-Немара вычисляется по формуле
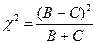
Нулевая гипотеза формулируется как Н0: P(A) = P(D).
Дата добавления: 2020-10-01; просмотров: 758;











