Графическое отображение вариационных рядов
Вариационный ряд по своей конструкции имеет 2 характеристики:
· значения варьирующего признака – варианты xi, i = 1,2,…,m;
· число случаев вариантов: абсолютные – частоты ni (fi), относительные – частости wi (относительные доли частот в общей сумме частот).
Тогда можно сказать, что вариационный ряд – это ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частостей).
Вариационные ряды по способу построения бывают дискретные и интервальные.
Дискретныйвариационный ряд можно рассматривать как такое преобразование ранжированного ряда, при котором перечисляются отдельные значения признака и указывается их частота.
Если число вариантов велико или признак имеет непрерывную вариацию, то строится интервальный вариационный ряд, в котором отдельные варианты объединяются в интервалы (группы). Принципы построения групп рассмотрены в разделе 2.4.Существуют следующие виды графического отображения вариационных рядов (рис. 3.1, 3.2):
· полигон для отображения дискретных рядов, когда фиксируются значения ( xi; ni, i = 1,2,…,m);
· гистограмма для отображения интервальных рядов (ki = х(i+1)– хi,
ni(wi));
· кумулята (кумулятивный ряд) – кривая накопленных частот.
Пример 3.1.
Построить графическое отображение вариационного ряда. Дано распределение рабочих механического цеха по тарифному разряду:
| Тарифный разряд, хi | Сумма | ||||||
| Количество рабочих (частота), ni | |||||||
| Частость, wi = ni/n | 0,04 | 0,06 | 0,12 | 0,5 | 0,18 | 0,1 |
Данный вариационный ряд является дискретным, его графическое отображение представлено: полигон (на рис. 3.1, а), кумулята (на рис. 3.2, а).
 | 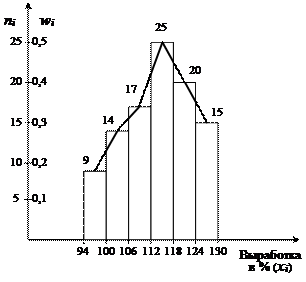 |
а) Дискретный вариационный ряд, б) Интервальный вариационный ряд,
(полигон) (гистограмма, полигон)
Рис. 3.1. Графическое отображение вариационных рядов
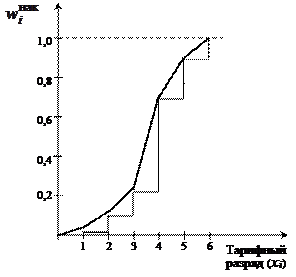 | 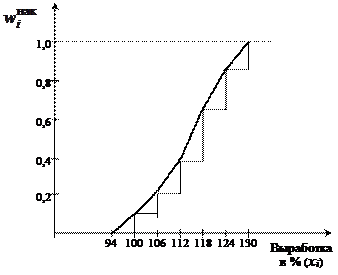 | ||
а) Дискретный вариационный ряд, б) Интервальный вариационный ряд,
(кумулята) (кумулята)
Рис. 3.2.Графическое отображение кумулятивного ряда
Дата добавления: 2020-10-01; просмотров: 753;











