Принципы построения статистических группировок
1. Выбор группировочного признака – признака, по которому производится разбиение совокупности на отдельные группы. В качестве признака необходимо использовать существенные обоснованные признаки. Группировочный признак – это основание (свойство объекта) для разделения объектов на группы.
Признаки различаются:
· по форме выражения (атрибутивные и количественные);
· по характеру колебания (альтернативные «да», «нет»; множественные);
· по роли во взаимосвязи явлений (результативные – могут меняться в зависимости от ситуации и целей анализа; факторные – воздействующие на другие признаки).
2. Определение количества групп. Если в основание группировки положен атрибутивный признак, то количество групп будет столько, сколько существует градаций (уровней) данного признака. Если основание группировки – количественный признак, то при определении количества групп в каждом конкретном случае следует исходить не только из степени колеблемости признака, но и из особенностей объекта и цели исследования.
Если совокупность состоит из большого числа единиц и распределение единиц по группировочному признаку близко к нормальному, для определения количества групп (m) используют формулу Стерджесса:
m = 1+3,322·lg N, (2.1)
где N – численность единиц совокупности.
Таблица 2.4 - Номограмма по формуле Стерджесса
| N | 15¸24 | 25¸44 | 45¸89 | 90¸179 | 180¸359 | 360¸719 | 720¸1489 |
| m |
3. Определение интервала группировки. Интервал – это значение варьирующего признака, лежащее в определенных границах.
Если вариация признака происходит в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами:
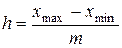 , (2.2)
, (2.2)
где h – величина интервала;
xmax, xmin – максимальное и минимальное значения группировочного признака в совокупности;
m – число групп.
Величина интервала округляется до ближайшего целого числа, или же кратного 10, 50, 100.
Возможны и другие варианты определения интервала группировки.
Интервалы могут быть двух видов:
· закрытыми, когда у интервала указаны обе границы;
· открытыми, когда у первого интервала указана верхняя граница, а у последнего – нижняя (например, в таблице 2.3, 1-я группа населения по размеру среднедушевого дохода – до 1000 руб.; последняя – 10000 и более).
Возможно построение вторичных группировок. Основные задачи, вторичной группировки:
· приведение данных к сопоставимым результатам;
· укрупнение интервалов;
· долевая перегруппировка (образование новых групп с меньшими интервалами).
Пример 2.1.
Имеются первичные данные о количестве работников определенного возраста.
| Возраст, лет | ||||||||||||||
| Число сотрудников |
Произведем группировку работников предприятия по возрасту. Для этого по формуле (2.1) рассчитаем число групп
m = 1+3,322·lg 39 = 6,28 ≈ 6.
Определим интервал группировки по формуле (2.2)
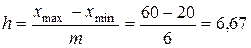 .
.
Округлим величину интервала до ближайшего целого h = 7.
Тогда группировка будет следующей:
| Возраст, лет | ||||||||||||||
| Число сотрудников | ||||||||||||||
| Границы интервалов | 20 – 27 | 27 – 33 | 33–40 | 40–47 | 47 – 54 | 54 – 60 | ||||||||
| Число сотрудников в интервале |
Граничное значение входит в тот интервал, где оно является верхней границей.
Произведем вторичную группировку с укрупнением интервалов (h = 10):
| Возраст, лет | ||||||||||||||
| Число сотрудников | ||||||||||||||
| Границы интервалов | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | ||||||||||
| Число сотрудников в интервале |
Вариационные ряды
При изучении совокупности интересующий нас признак у различных единиц совокупности принимает различные значения, т.е. он имеет некоторую вариацию.
Вариацией признака называется наличие различий в численных значениях признаков у отдельных единиц совокупности.
Чтобы выявить характер распределения единиц совокупности по варьирующим признакам, определить закономерности в этом распределении, строят ряды распределения единиц совокупностей по какому-либо варьирующему признаку.
Ряды распределения, построенные по количественному признаку называются вариационными.
При анализе вариационных рядов решают следующие задачи:
1) Определение меры вариации, т.е. количественное измерение степени колеблемости признака. Это позволяет сравнивать различные совокупности между собой по степени рассеяния и отслеживать уровень вариации признака одной и той же совокупности в различные периоды.
2) Исследование закономерностей вариации в статистических совокупностях для изучения причин, вызывающих вариацию.
Для описания статистических распределений обычно используются следующие виды характеристик (показателей):
1) средние величины;
2) характеристики вариации (рассеяния);
3) характеристики дифференциации и концентрации;
4) характеристики формы распределения.
Дата добавления: 2020-10-01; просмотров: 729;











