Вычисление интегралов
Для вычисления интегралов используются функции:
| Вычисляемая форма: | Инертная форма: |
| int(f,x) | Int(f,x) |
| int(f,x=a..b) | Int(f,x=a..b) |
| int(f,x=a..b,continuous) | Int(f,x=a..b,continuous) |
где f – подынтегральная функция,
x – переменная интегрирования,
a и b – нижний и верхний пределы интегрирования,
continuous – опционально заданное условие.
Maple старается найти аналитическое значение интеграла. Если это не удается, то возвращается исходная запись интеграла. В этом случае для вычисления определенного интеграла надо использовать функцию evalf(int(f,x=a..b)).
>Int(sin(x),x)=int(sin(x),x);
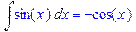
>Int(a*x^n,x)=int(a*x^n,x);
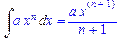
>Int(ln(x)^3,x)=int(ln(x)^3,x);
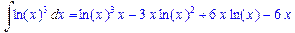
В отличие от функции дифференцирования, для функции интегрирования нельзя задавать подынтегральную функцию в виде списка или множества, однако возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов.
>sum(int(x^i,x),i=1..5);
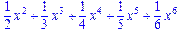
>int(sum(x^i,i=1..5),x);
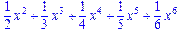
>P(x):=a*x^3+b*x^2+c*x+d;
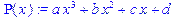
>int(P(x),x);
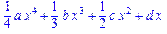
Если Maple не может вычислить интеграл, то можно попытаться найти его значение в виде многочлена
>int(exp(x^4),x);
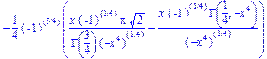
>convert(taylor(%,x=0,10),polynom);
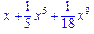
Для вычисления определенных интегралов, необходимо указывать пределы интегрирования.
>Int(x^1.5,x=0..5)=int(x^1.5,x=0..5);
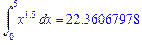
>Int(x*exp(-x),x=0..infinity)=
int(x*exp(-x),x=0..infinity);
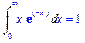
Опция continuous, добавленная в качестве четвертого аргумента команды, вынуждает Maple игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования.
>Int(1/(x-1)^2,x=0..2)=
int(1/(x-1)^2,x=0..2,continuous);
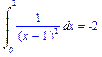
Для вычисления кратных интегралов функции int и Int нужно применять неоднократно:
>Int(Int(x^2*y^2,x),y)=int(int(x^2*y^2,x),y);
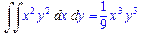
В качестве пределов интегрирования могут быть функции:
>Int(Int(2-x-y,x=sqrt(y)..y^2),y=0..1)=
int(int(2-x-y,x=sqrt(y)..y^2),y=0..1);
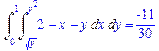
Если значение интеграла нельзя найти в аналитическом виде, можно получить его значение с заданной точностью:
>Int(1/(exp(x^2)+x),x=0..1)=
int(1/(exp(x^2)+x),x=0..1);
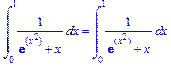
>evalf(%,20);
.58592031278103454744=.58592031278103454744
>evalf(%);
.5859203128=.5859203128
Дата добавления: 2020-10-01; просмотров: 429;











