Разложение функций в ряд
Для разложение функции в ряд служат следующие функции:
series (f,eqn)
series (f,eqn,n)
где f – разлагаемая функция,
eqn – условие (например, в виде x=a) или имя переменной,
n – необязательное и неотрицательное целое число, задающее число членов ряда (по умолчанию n=6, но может переустанавливаться системной переменной Order).
Если в качестве eqn задано имя переменной, это соответствует разложению по этой переменной в области x=0. Задав eqn в виде x=a можно получить разложение по переменной x в окрестности точки x=a.
Разложение получается в форме степенного многочлена. остаточная погрешность задается членом вида O(xn). При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert.
>series(sinh(x),x);
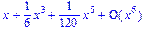
>series(sinh(x),x,10);
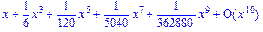
>series(2*x^2-x,x=5,10);
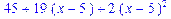
>f:=sin(x)/x;
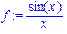
>p:=series(f,x,8);
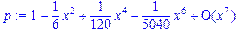
Для разложения в рядТейлора используется функция:
taylor (f,eqn,n)
где f – разлагаемая функция,
eqn – условие (например, в виде x=a) или имя переменной,
n – необязательное и неотрицательное целое число, задающее число членов ряда (по умолчанию n=6).
Задав eqn в виде x=a можно получить разложение по переменной x в окрестности точки x=a. Если в качестве eqn задано имя переменной, то разложение ищется в окрестности точки x=0, т.е. фактически вычисляется рядМаклорена.
>taylor(1-exp(x),x=1,4);
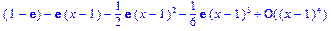
Для разложения в ряд Тейлора функции нескольких переменных используются функции:
mtaylor(f,v)
mtaylor(f,v,n)
mtaylor(f,v,n,w)
где f – разлагаемая функция,
v – список имен или равенств,
n – необязательное число, задающее порядок разложения,
w – необязательный лист целых чисел, задающих «вес» каждой переменной списка v.
Эта функция должна вызываться из библиотека Maple.
>readlib(mtaylor):
>mtaylor(sin(x*y),[x,y],10);
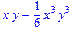
Для вычисления асимптотическихразложений функций (в виде рядов) используются функции:
asympt(f,x)
asympt(f,x,n)
где f – разлагаемая функция,
x – имя переменной, по которой производится разложение,
n – необязательное число, задающее порядок разложения.
>asympt(x/(1-x^2),x);
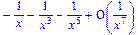
Дата добавления: 2020-10-01; просмотров: 521;











