Динамика качения колеса по недеформируемой поверхности

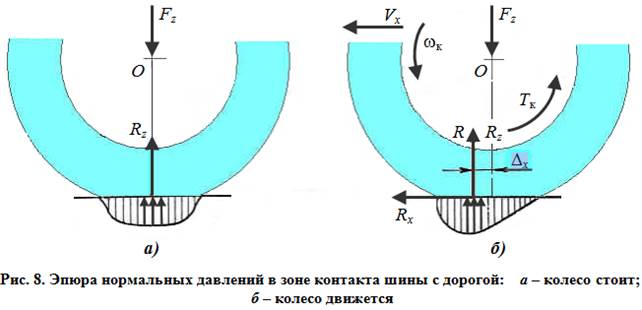
Со стороны шасси автомобиля на колесо действуют силы F_x и F_z , а также момент Т_к (рис. 7). Вертикальная сила F_z направлена вниз и является резуль-татом воздействия на подшипники колеса приходящейся на него массы автомобиля. Горизонтальная сила F_x в зависимости от режима движения колеса может иметь направление, совпадающее с направлением движения автомобиля (вектор скорости V_x) или противоположное ему. Момент Т_к подводится к ведущему колесу от полуоси, этот момент совпадает с направлением вращения колеса и поэтому считается положительным. Если момент Т_к подводится от тормозного механизма, его направление противоположно вектору угловой скорости колеса w_к , и он считается отрицательным. Возможна также ситуация, когда Т_к = 0.

Нормальная реакция от поверхности дороги R_z направлена вверх, причем точка ее приложения у катящегося колеса с эластичной шиной смещена вперед на величину D_х относительно проекции оси вращения колеса на опорную поверхность. Это смещение обусловлено существенным отличием эпюры нормальных давлений в зоне контакта шины с дорогой у неподвижного колеса (эпюра давлений симметрична относительно вертикальной оси колеса и равнодействующая реакция R_z совпадает с этой осью, см. рис. 8, а) и у движущегося

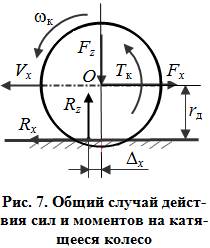
колеса (эпюра давлений несимметрична вертикальной оси колеса, реакции со стороны дороги больше в набегающей области, чем в

сбегающей, что приво-

дит к смещению равнодействующей R_z вперед, см. рис. 8, б).

Продольная реакция R_x поверхности дороги расположена в плоскости дороги и является положительной, если она совпадает с направлением движения колеса, т.е. с вектором V_x .

Уравнение сил, описывающее движение колеса, имеет вид

m_к а_к = R_x - F_x или R_x = F_x + m_к а_к , (7)

где m_к – масса колеса ; а_к - ускорение поступательного движения колеса.

Соответственно уравнение моментов относительно точки О колеса

J_к Е_к = Т_к - R_z D_x - R_x r_д

или Т_к = R_z D_x + R_x r_д+ J_к E_к , (8)

где J_к – момент инерции колеса относительно оси его вращения ; Е_к – ускорение вращательного движения колеса.

Из выражения (8) получим

R_x = T_к / r_д - R_z D_x /r_д- J_к Е_к / r_д . (9)

Мощность (Р_к), подводимая к колесу, определится из выражения

Р_к = Т_к w_к . (10)

Колесо преобразует вращательное движение в поступательное, при этом, как при всяком преобразовании, происходят потери мощности. Эти потери определяются разностью между мощностью Р_к , подводимой к колесу, и мощностью Р_ав , передаваемой от колеса к автомобилю, т.е.

Р_f = P_к - Р_ав , (11)

где Р_f – мощность потерь при качении колеса или мощность сопротивления качению колеса.

Рис.8. Эпюра нормальных давлений в зоне контакта шины с дорогой: а) колесо неподвижно; б) колесо движется

Рис.8. Эпюра нормальных давлений в зоне контакта шины с дорогой: а) колесо неподвижно; б) колесо движется

Если рассмотреть режим движения с постоянной скоростью (V_x = const), то Е_к = 0 и , поскольку Р_ав = F_x V_x = R_x V_x , с учетом выражения (9) получим

Р_ав = ( Т_к / r_д - R_z D_х / r_д) w_к r_к . (12)

Подставим выражения (10) и (12) в формулу (11). Тогда мощность сопротивления качению колеса определится как

Р_f = T _к w_к - (Т_к / r_д - R_z D_x / r_д ) w_к r_к =

= [ T_к (r_д - r_к) / r_д + R_z D_х r_к / r_д ] w_{к .} (13)

Отношение Р_f / w_к = T_f называют моментом сопротивления качению колеса, а отношение Р_f / V_x = F_f – силой сопротивления качению колеса.

Условную количественную характеристику f = F_f / R_z называют коэффи- циентом сопротивления качению колеса.

Принимая во внимание равенство (13) развернем выражение f = F_f / R_z , помня, что F_f =P_f / V_x = Р_f / w_к r_к . Получим

f = D_х / r_д + Т_к (r_д - r_к) / R_z r_д r_к = f_c + f_к , (14)

где f_c = D_x / r_д – составляющая коэффициента сопротивления качению, характе-ризующая силовые потери, обусловленные смещением нормальной реакции R_z вперед и возникновением момента, противодействующего качению колеса (при отсутствии буксования является главной составляющей этого коэффициента);

f_к = Т_к (r_д – r_к) / R_z r_дr_к – составляющая коэффициента сопротивления качению, характеризующая кинематические потери, вызванные изменением радиуса качения колеса при передаче тягового момента (основное влияние на величину коэффициента сопротивления качению оказывает при существенном буксовании колеса).

В процессе качения колесо автомобиля (колесной машины) находится в одном из следующих режимов: ведущем, свободном, нейтральном, ведомом, тормозном. Для характеристики режима качения колеса используем уравнение силового баланса (9), несколько трансформировав его с учетом выводов формулы (14)

R_x = T_к / r_д – R_z f_c - J_к Е_к / r_д . (9¢)

1. Ведущим называют режим качения колеса, при котором оно приводится во вращение моментом Т_к , совпадающим по направлению с вектором w_к , при этом действующая на ось колеса продольная сила F_х (реакция корпуса автомобиля) противоположна направлению движения, т.е. противоположна вектору V_х (см. рис.7). Режим возможен только при R_х > 0 и, как следует из выражения (9¢),

Т_к > R_z f_c r_д + J_к Е_к > 0 .

2. Свободным называют режим качения колеса, при котором оно приводится во вращение моментом Т_к , совпадающим по направлению с вектором w_к , а продольная сила F_х равна нулю (рис. 9, а).

Следовательно, на указанном режиме F_х = 0 ; R_х = 0 и выражение (9¢) превращается в

Т_к = R_z f_c r_д + J_к Е_к > 0 .

3. Нейтральным называют режим качения колеса, при котором оно приводится во вращение моментом Т_к , совпадающим по направлению с вектором w_к , и продольной силой F_х , совпадающей по направлению с вектором V_х (см. рис. 9, б).

Здесь Т_к > 0, а R_х < 0, ( она поменяла направление по сравнению с режимом ведущим ). Тогда

0 < Т_к < R_z f_c r_д + J_к Е_к .

4. Ведомым называют режим качения колеса, при котором оно приводится во вращение продольной силой F_х , направление которой совпадает с вектором V_х , а крутящий момент Т_к равен нулю (см. рис. 9, в). Следовательно, при этом F_х = R_x < 0 , а Т_к = 0 и соответственно из выражения (9¢) получим

R_х = - [ R_z f_c + J_к Е_к / r_д ] < 0 .

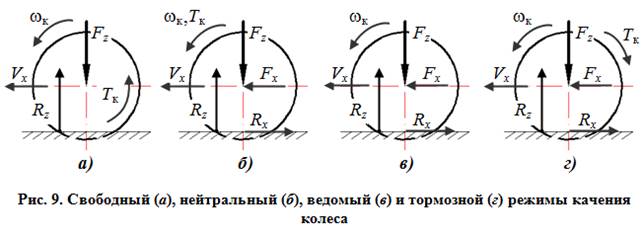
5. Тормозным называется режим качения колеса, при котором оно приводится во вращение продольной силой F_х , направление которой совпадает с вектором V_х , и одновременно оно испытывает действие момента Т_к , направленного противоположно вектору w_к (рис. 9, г ). В этом случае F_х < 0 , R_х < 0 , Т_к < 0, причем

R_х = - [ Т_к /r_д + R_z f_c + J_к Е_к / r_д ] .

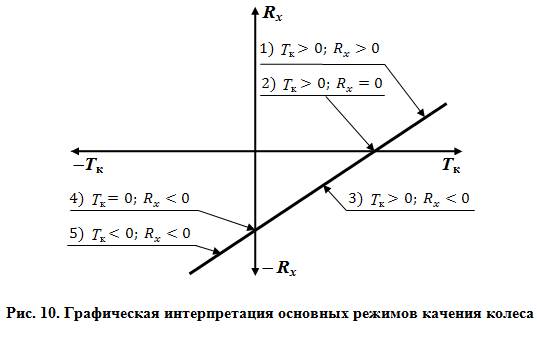
Все перечисленные режимы качения колеса наглядно иллюстрирует гра-

фик зависимости R_х от Т_к (рис. 10).