Идеальные реакторы для изучения кинетики клеточного роста

Если небольшое количество живых клеток поместить в раствор, содержащий все необходимые питательные вещества, то при определенных температуре и рН клетки будут расти. В зависимости от морфологии клетки процесс ее роста может происходить двумя путями. Одноклеточные организмы претерпевают в процессе роста деление, и поэтому увеличение их биомассы (массы живых организмов) сопровождается увеличением числа клеток. Основное внимание в настоящей главе будет уделено именно этому типу роста; здесь мы встретимся с проблемой роста популяции. Совершенно по-иному происходит рост плесневых грибов — в этом случае по мере роста организма возрастают в первую очередь длина и число гиф мицелия. Таким образом, в культуре растущей плесени увеличиваются размеры организмов и их концентрация, но не обязательно число организмов.

С клеточным ростом тесно связаны два других процесса: поглощение клеткой некоторых веществ из окружения и выделение конечных продуктов метаболизма клетки в среду. Как мы увидим ниже, в процессе роста скорости этих процессов изменяются в очень широких пределах. В общем случае предсказать эти скорости не представляется возможным; вместе с тем весь многолетний опыт говорит о том, что среди множества известных процессов с участием культур клеток достаточно часто встречается только ограниченное число типичных путей утилизации субстрата и образования продуктов жизнедеятельности клеток. Изучив сначала эти типичные пути, мы будем лучше подготовлены к решению новых задач, связанных с применением культур растущих клеток.

Необходимая и достаточная точность (а следовательно, и сложность) математического описания кинетических свойств системы в свою очередь зависит от ее сложности и предполагаемой области применения математических выражений. Прежде чем перейти к анализу конкретных процессов и соответствующих математических выражений, описывающих их кинетику, мы должны иметь определенное представление о разнообразии реакций и процессов в популяции клеток. В нашем обсуждении основное внимание будет уделено клеточному росту, но аналогичные принципы, концепции и ход рассуждений применимы и к другим аспектам изучения химических процессов в клетке.

Начнем с самого сложного случая — с анализа растущей популяции клеток в самом общем виде. Затем рассмотрим, какие упрощения можно допустить в этом анализе и в каких ситуациях эти упрощения оправданны. На рис. 7.1 перечислены некоторые параметры, явления и взаимодействия, влияющие на кинетику роста популяции клеток.

При этом прежде всего следует усвоить, что во всех случаях нужно учитывать две взаимодействующие системы — биологическую фазу, состоящую из популяции клеток, и фазу, окружающую эту популяцию, или среду. Клетки поглощают питательные вещества и превращают субстраты (взятые из среды) в продукты метаболизма. Клетки генерируют теплоту, а температура среды в свою очередь определяет температуру клеток. Среда оказывает механическое воздействие на клетки посредством гидростатического давления или гидродинамических эффектов, а также путем изменения вязкости среды вследствие накопления клеточной массы и продуктов жизнедеятельности клеток.

Что касается среды, то из ряда ее важнейших характеристик прежде всего следует отметить многокомпонентноcть: во-первых, она должна содержать все необходимые для роста клеток питательные вещества, и, во-вторых, в ней накапливаются (по мере роста клеток) различные конечные продукты клеточного метаболизма. Химические реакции могут происходить и в среде, что приводит к модификации продуктов метаболизма, как, например, при гидролизе пенициллина. Часто клетки потребляют или продуцируют вещества, изменяющие кислотность среды; взаимосвязь клеточных процессов с кислотно-основным равновесием определяет рН среды, который в свою очередь влияет на клеточную активность и на процессы транспорта. В ходе клеточных реакций могут происходить изменения температуры, ионной силы, рН и реологических свойств бульона во времени.

Часто среда представляет собой многофазную систему, состоящую из жидкой фазы и диспергированных в ней пузырьков газа или из двух несмешивающихся жидких фаз, а иногда из одной газовой и двух жидких фаз. К числу последних достижений в разработке биореакторов относятся методы одновременного проведения клеточных реакций и процессов разделения путем введения в среду особых веществ, способствующих образованию дополнительной жидкой или твердой фазы. Наконец, в силу большого объема биологического реактора, высокой вязкости и неньютоновской природы бульона в отдельных его точках могут создаться разные условия. Все эти параметры и переменные среды существенно влияют на кинетику клеточного роста.

Что же касается наиболее важных особенностей популяции клеток, то, как мы уже знаем из предыдущих глав, каждая индивидуальная клетка представляет собой сложную многокомпонентную систему, которая даже на клеточном уровне далека от гомогенности. В каждой клетке одновременно осуществляется множество химических реакций, управляемых сложным комплексом систем регуляции. Благодаря этим системам клетка может изменять (и изменяет на самом деле) скорость и даже тип происходящих в ней химических реакций в зависимости от условий и состава среды. Длительное культивирование клеточной популяции может сопровождаться накоплением спонтанных мутаций; кроме того, особенности технологического процесса могут налагать давление отбора, приводящее к медленным изменениям генетической природы штамма.

С другой стороны, в культуре растущих клеток всегда наблюдается существенная гетерогенность популяции, т.е. в любой момент, в любом, даже самом малом объеме культуры индивидуальные клетки различаются по возрасту (одни только что образовались в результате деления, другие уже достигли состояния зрелости, а третьи находятся в стадии деления) и, следовательно, по биохимической активности.

Очевидно, практически невозможно создать кинетическую модель, которая учитывала бы все параметры и факторы, перечисленные на рис. 7.1. Поэтому теперь рассмотрим ряд приближений, которые позволяют упростить эту картину и найти математические выражения, описывающие кинетику роста популяции клеток.

Во-первых, что касается среды, то обычно допускают, что, за исключением одного компонента, все ее составляющие присутствуют в таких высоких концентрациях, что их изменения практически не отражаются на общих скоростях процессов. Таким образом, один компонент среды становится питательным веществом, лимитирующим скорость клеточного роста, и при анализе влияния состава среды на кинетику роста клеток мы должны учитывать концентрацию только этого компонента. Иногда возникает необходимость в учете некоторых других составляющих среды, например накапливающегося в среде ингибитора, в противном случае наше описание кинетики было бы слишком далеким от истинной картины. В отношении других параметров среды часто можно допустить, что их изменения не влияют в сколько-нибудь существенной степени на кинетику роста микроорганизмов за тот период, в течение которого проводится типичный эксперимент или осуществляется типичный процесс, если эти изменения не превышают обычных для этого эксперимента или процесса пределов. К тому же системы контроля и регулирования биореакторов могут поддерживать на постоянном уровне целый ряд параметров среды, в том числе рН, температуру и концентрацию растворенного кислорода. Впрочем, в некоторых случаях для адекватного описания требуемого диапазона кинетического поведения может возникнуть необходимость учета в модели многокомпонентности и нескольких параметров среды.

На рис. 7.2 суммированы основные принципы различных приближений и способов описания, которые могут быть полезны при математическом анализе клеточной фазы системы. Согласно этой схеме, разработанной Фредриксоном и Цучия, подходы к анализу микробиологических систем классифицируются в соответствии с числом компонентов, используемых при описании клеток, а также в зависимости от того, рассматриваются ли клетки как гетерогенная популяция различных объектов (как оно и есть на самом деле) или как популяция некоторых усредненных клеток (в этом случае клетки принципиально не отличаются от какого-либо компонента в растворе). Многокомпонентные модели клеток называют структурированными, а однокомпонентные - неструктурированными. Описание популяции клеток с учетом их гетерогенности называют сегрегированным подходом, а в несегрегированном описании рассматривают только усредненные свойства клеток.

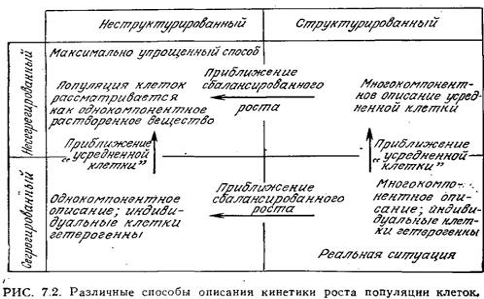
Как показано на рис. 7.2, реальная ситуация отвечает структурированной сегрегированной системе. Если гетерогенность клеток не влияет в существенной степени на кинетику исследуемых процессов, то можно принять «приближение усредненной клетки» и тем самым упростить способ описания от сегрегированного до несегрегированного. В так называемом состоянии «сбалансированного роста» вся синтетическая активность клеток скоординирована таким образом, что на средний состав клеток пролиферация популяции не влияет. В этом случае допустимо использовать модели, не учитывающие многокомпонентную природу клеток. Как мы увидим ниже, при анализе и описании роста популяций клеток обычно принимают наиболее идеализированную ситуацию, т. е. несегрегированную, неструктурированную модель.

С другой стороны, мы познакомимся с рядом таких ситуаций, когда выгоднее рассматривать биологическую фазу как более сложную систему. Так, в нестационарном состоянии (типичном, в частности, для периодических микробиологических процессов) условия сбалансированного роста даже в первом приближении соблюдаются только в течение сравнительно короткого промежутка времени. Хорошо известно, что в ходе периодического процесса в очень широких пределах могут изменяться как клеточный состав популяции, так и скорости и типы реакций, осуществляющихся в этой популяции, и тогда могут пригодиться более детальные модели. Кроме того, структурированные модели позволяют отражать непосредственно в математических выражениях известные особенности сети клеточных биохимических реакций. Аналогично не представляющее особых затруднений включение в модель кинетики клеточного роста особенностей клеточного цикла (сегрегированный подход) способствует повышению ценности и расширению диапазона применимости модели. Важнейшими элементами сегрегированных моделей являются кинетика и особенности регуляции роста индивидуальной клетки.

Живые клетки представляют собой чрезвычайно малые системы, поэтому количество любого химического компонента в них крайне ограничено. Действительно, приведенные в табл. 5.6 величины очень малы по сравнению с обычным для химика числом молекул порядка 10²³. Предельным случаем является ДНК, которая в медленно растущей бактерии содержится только в количестве одной молекулы; очевидно, что в этом случае само понятие «концентрация ДНК в клетке» становится весьма неопределенным. То же самое можно сказать о содержащихся в следовых количествах ионах, органоидах и многих других компонентах клетки. Хотя в некоторых из рассматриваемых ниже моделей мы будем описывать внутриклеточные события как непрерывные, следует отдавать себе отчет в том, что такое описание является всего лишь удобным приближением типичной усредненной клетки в популяции клеток (см. ниже). Реакции и процессы массопередачи, в которых участвует ограниченное число молекул, должны рассматриваться как случайные события. Для описания таких событий создавались стохастические модели популяций клеток, не имеющих существенных преимуществ по сравнению с более простыми детерминистическими моделями. Предсказуемость поведения популяции клеток можно проиллюстрировать, например, оценив точность детерминистического описания очень малой популяции, в частности типичного инокулята (посевного материала; обычно около 10⁵ клеток). Пусть совокупность продолжительностей клеточных циклов индивидуальных клеток описывается нормальным распределением:

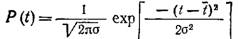
Примем t=1, а стандартное отклонение Ϭ равным 0,5. Тогда мы можем сказать, что с коэффициентом доверительности 0,95 продолжительность клеточного цикла отдельной клетки составляет одна клетка = t± 1,96 Ϭ = 1,0±0,98

Далее рассмотрим суспензию, содержащую достаточно большое число клеток, например m клеток. Пусть каждая из m клеток растет независимо от других клеток, т. е. клеточная суспензия содержит m независимых образцов. Тогда 95%-ный доверительный предел времени удвоения численности этой популяции будет равен 2 Ϭ. Популяция, где

Следовательно, с возрастанием m неопределенность времени удвоения численности популяции быстро уменьшается. Приняв, например, как и раньше, Ϭ = 0,5 и t=l,0, легко найти, что 95%-ные доверительные пределы для t в случае популяции из m клеток составляют

В сущности, этот несложный расчет еще раз подтверждает известное положение, что, как и в любых стохастических процессах при относительно большом числе событий (например, в химических реакциях или в явлениях, связанных с транспортом жидкостей), изменения характеристик популяции могут быть предсказаны с достаточно большой точностью, даже если стандартные отклонения характеристик индивидуальных клеток велики. Так, рост инокулята, приводящий к повышению концентрации с 10⁴ до 10⁸ клеток в 1 мл, очевидно, обеспечивает достаточное усреднение по всем стадиям роста, что позволяет с высокой точностью определить время удвоения численности популяции.

Точно так же можно достаточно обоснованно говорить о скорости синтеза ДНК в типичной клетке популяции, хотя в каждой индивидульной клетке синтезируется только одна или две молекулы ДНК со скоростью, которая в данный момент может резко отличаться от средней величины.

Невозможно обсуждать кинетику в отсутствие данных о конструкции реактора для измерения скоростей процессов и оценки их кинетики. В следующем разделе мы вкратце рассмотрим соответствующие материальные балансы для двух типов идеальных биореакторов. Затем мы приступим к анализу кинетики клеточного роста, начиная с ситуации, схематично изображенной в верхнем левом углу рис. 7.2, т. е. с простейших моделей кинетики клеточного роста, утилизации субстрата и образования продуктов метаболизма. В последующих разделах главы мы изучим другие ситуации, также изображенные на рис. 7.2, и попытаемся оценить важность различных концептуальных и математических подходов к анализу кинетики роста популяции клеток. В общем случае разработка кинетической модели популяции клеток является своего рода искусством, требующим, во-первых, учета окончательной цели, для которой эта модель предназначается, во-вторых, тщательно продуманного и обоснованного выбора основных переменных и параметров, влияющих на наиболее важные процессы, и, в-третьих, известной концептуальной и математической гибкости, что необходимо для перевода качественных характеристик системы на язык применимых в практической деятельности математических выражений.

Получить полезную информацию о кинетике роста популяции микроорганизмов практически невозможно, если условия в разных участках объема реактора не идентичны. Поэтому желательно изучать кинетику только в реакторах с полным перемешиванием. Здесь мы изучим реакторы с полным перемешиванием периодического действия и проточные (непрерывного действия) реакторы.