Идеальный проточный реактор с полным перемешиванием (ПРПП)

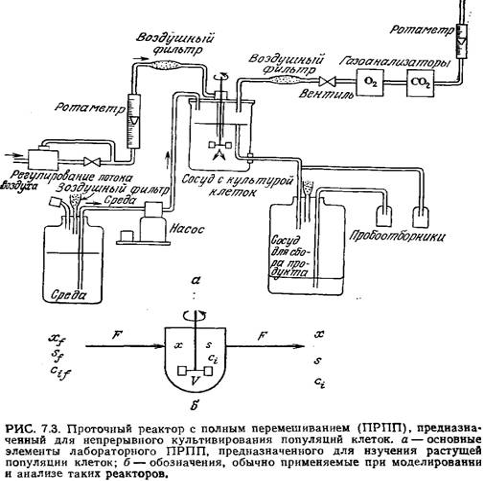На рис. 7.3, а изображены основные узлы лабораторного проточного реактора с полным перемешиванием (ПРПП), а на рис. 7.3, б указаны основные обозначения, используемые при моделировании и анализе такого рода реакторов. Если эти реакторы предназначены для изучения роста культур клеток, то их часто называют хемостатами. Как показано на этих рисунках, перемешивание осуществляется с помощью мешалки, потока восходящих пузырьков газа или того и другого. Примем, что в ПРПП перемешивание культуральной жидкости осуществляется настолько эффективно, что каждая фаза содержимого реактора вполне однородна по составу, т.е. концентрации любых компонентов в любой из фаз одинаковы во всем объеме реактора. Как показано на схеме, отсюда следует важный вывод о том, что состав вытекающего потока не отличается от состава содержимого реактора.

Полное перемешивание должно обеспечивать и одинаковую концентрацию растворенного кислорода во всем объеме жидкой фазы. Этот факт особенно важен при анализе аэрируемых ПРПП, поскольку отсюда следует, что в большинстве случаев мы можем изучать происходящие в реакторе процессы независимо от конструкций аэратора или мешалки. Если система аэрации обеспечивает такую концентрацию растворенного кислорода, которая не лимитирует клеточный рост в ПРПП, то анализ кинетики клеточного роста мы можем рассматривать как независимую проблему. Аналогичные соображения применимы и к проблемам теплопередачи, которые могут возникать, в ходе роста микроорганизмов. Систему можно считать изотермической, если реактор снабжен устройствами для полного перемешивания, эффективного отвода тепла и регулирования температуры на заданном уровне; тогда можно изучать процессы микробиологических превращений в изотермических условиях.

В большей части последующего материала мы будем принимать все указанные допущения. В стационарном состоянии, когда концентрации всех компонентов в реакторе не изменяются во времени, к любому компоненту системы применимо следующее уравнение:

Обозначив, как и раньше, символом V_R общий объем культуры в реакторе, указанное уравнение стационарного состояния можно записать в следующем виде:

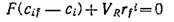
где F — объемная скорость потока раствора питательных веществ и вытекающего потока; с_if — молярная концентрация компонента i в потоке питательных веществ; с_i — концентрация компонента i в реакционной смеси и вытекающем потоке. Преобразовав уравнение (7.5),

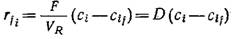
можно без труда определить скорость образования компонента i, измерив его (стационарные) концентрации на входе в реактор и на выходе из него. Введенный в уравнение (7.6) параметр D называют скоростью разведения и определяют в виде

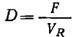
Этот параметр определяет время пребывания или скорость переработки в реакторе и равен числу объемов жидкой фазы реактора, проходящей через него в единицу времени. Параметр D представляет собой величину, обратную более обычным в химической технологии параметрам среднего времени пребывания или среднего времени удерживания. Здесь, однако, мы будем пользоваться общепринятым в литературе по биохимической технологии понятием о скорости разведения.

Из сравнения уравнений (7.3) и (7.6) нетрудно заметить, что кинетика процессов в ПРПП проще, чем в реакторе периодического действия; действительно, здесь нет необходимости в определении зависимости концентрации от времени и в последующем дифференцировании полученных данных. Изучение кинетики роста популяции клеток в этих условиях имеет еще одно преимущество, заключающееся в том, что в ПРПП клетки могут приспособиться к стационарным условиям и таким путем перейти в состояние сбалансированного или почти сбалансированного роста. Этим самым создается реальная возможность для обеспечения относительно определенного, воспроизводимого состояния клеточной популяции; в случае периодических процессов с участием микроорганизмов решить эту задачу значительно труднее. С другой стороны, эксперименты по изучению роста клеток в периодических процессах могут быть выполнены в небольших сосудах, размещенных на термостатированной качалке; оборудование для ПРПП значительно сложнее и дороже. Состояние стационарности в биологических ПРПП может быть достигнуто только через несколько часов или даже дней, что существенно повышает опасность внесения загрязнений, обесценивающих результаты эксперимента. Наконец, в крупномасштабном производстве в ряде случаев, вероятно, более целесообразными окажутся периодические процессы, отличающиеся непостоянным, несбалансированным ростом, различными метаболическими процессами и активностями в разные периоды процесса; для таких производств кинетические модели, основанные на стационарных условиях в ПРПП, могут оказаться вообще непригодными. Отсюда следует, что экспериментальному изучению кинетики роста популяций клеток микроорганизмов и высших организмов и разработке соответствующих математических выражений должно предшествовать точное определение предполагаемой сферы применения этих выражений. Это требование является основой для разработки программ экспериментального и математического моделирования.

В следующем разделе мы рассмотрим простейшие модели роста популяций клеток. При этом основное внимание мы будем уделять кинетике роста клеток в ПРПП, поскольку основные принципы построения кинетических уравнений были разработаны и наиболее полно развиты именно в экспериментах с хемостатами.