Уравнение Моно для кинетики клеточного роста

Приведенная на рис. 7.4 зависимость характерна только для тех случаев, когда удельная скорость клеточного роста не зависит от х и s. [Здесь под s мы понимаем массовую концентрацию субстрата, лимитирующего клеточный рост.] Система становится определенной, если скорость роста клеток лимитируется каким-либо питательным веществом.

Прежде чем перейти к обсуждению деталей зависимости скорости роста от подачи питательных веществ, рассмотрим общие теоретические и практические пути создания сред для культивирования клеток.

В зависимости от состава различают два типа сред. Синтетическими называют среды с четко определенным химическим составом. Как показано в табл. 7.1, такие среды создаются на основе раствора неорганических солей, к которому добавляют необходимые источники углерода, азота и энергии, а также все незаменимые витамины. Неорганические соли служат не только источником ионов, необходимых для нормального функционирования клеток, но и выполняют буферную функцию, сглаживая большие флуктуации рН в процессе роста популяций. Сложные среды содержат материалы неопределенного состава. Например, среда 4 в табл. 7.1 относится к сложным, поскольку точный химический состав дрожжевого экстракта неизвестен. В состав других сложных сред входят мясной бульон, кровяной бульон, кукурузный экстракт и сточные воды.

Основное требование, предъявляемое к среде, заключается в обеспечении высокой скорости роста клеток и(или) синтеза продуктов их жизнедеятельности.

Отсюда, однако, отнюдь не следует (как можно было бы предположить чисто интуитивно), что все питательные вещества нужно подавать в большом избытке. Во-первых, избыточная концентрация питательного вещества может ингибировать рост клеток или даже привести к их гибели. Во-вторых, если клетки растут слишком интенсивно, то накапливающиеся конечные продукты метаболизма могут нарушить нормальные биохимические процессы в клетках. Поэтому обычно общий рост клеток лимитируют, ограничивая количество одного питательного вещества в среде.

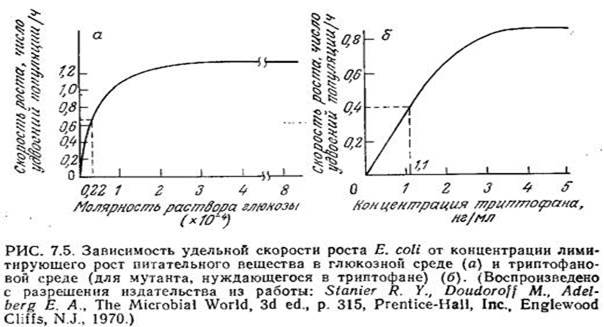
Если концентрация одного незаменимого компонента среды изменяется, а концентрации всех других компонентов остаются без изменения, то, как это показано на рис. 7.5, зависимость скорости клеточного роста от концентрации незаменимого питательного вещества обычно выражается кривой типа гиперболы. Математическое выражение, отражающее функциональную зависимость удельной скорости клеточного роста р, от концентрации незаменимого питательного вещества, было предложено Моно в 1942 г. Уравнение Моно имеет ту же форму, что и уравнение изотермы адсорбции Ленгмюра (1918 г.) и обычное уравнение скорости катализируемой ферментом реакции с одним субстратом, предложенное Анри (1902 г.) и Михаэлисом. и Ментен (1913 г.), и устанавливает, что

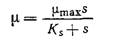
В этом уравнении µ_max — максимальная скорость роста, достигаемая при s>Ks и постоянных концентрациях всех других незаменимых питательных веществ. Ks — это такая концентрация лимитирующего клеточный рост питательного вещества, при которой удельная скорость роста вдвое ниже максимального значения. В первом приближении можно считать, что Ks представляет собой промежуточную зону между диапазоном низких концентраций, при которых µ линейно зависит от s, и диапазоном высоких концентраций, когда µ становится независимым от s. Как показано на рис. 7.5, значения Ks для штаммов Е. coli, растущих в лимитируемых глюкозой и триптофаном средах, составляют 0,22-10^{-4 М и 1,1 нг/мл соответственно.}

Поскольку мы уже знакомы с биохимией клетки, для нас должно быть очевидно, что уравнение Моно, скорее всего, чрезмерно упрощено. Как, однако, это часто бывает и в других областях технологии, относительно простое уравнение иногда удовлетворительно описывает определенные зависимости, хотя физический смысл параметров модели неизвестен или, возможно, даже, вообще не существует. Впрочем, в некоторых специфических ситуациях уравнению Моно можно приписать определенный физический смысл. Одна из наиболее показательных ситуаций такого типа складывается тогда, когда скорость клеточного роста лимитируется скоростью транспорта через мембрану при участии пермеаз (вспомните разд. 5.7).

В уравнении Моно (7.10) привлекает его простота, однако применение этого простого выражения требует от исследователя большой осторожности. Во-первых, величина Ks часто довольно мала, поэтому s обычно намного больше Ks и выражение s/(Ks + s) можно рассматривать как адекватное выражению для расчета отклонений µ от µ_mах по мере снижения концентрации s. Это соотношение предполагает также, что удельная скорость роста р, не равна нулю при любых отличных от нуля концентрациях лимитирующего скорость клеточного роста компонента. В общем случае данное условие нельзя считать доказанным для s<Ks.

Если скорость роста популяции клеток связана с концентрацией лимитирующего клеточный рост питательного вещества математическим выражением типа уравнения Моно, то отсюда следует, что между условиями работы реактора и кинетическими и стехиометрическими параметрами популяции клеток должны существовать определенные зависимости. Для выявления этих зависимостей можно начать с уравнения материального баланса по лимитирующему клеточный рост субстрату, связанного с балансом по, клеточной массе, поскольку ц зависит от s. В балансе по субстрату мы будем использовать экономический коэффициент Ух/s (см. разд. 5.10.1):

Уравнения (7.14) и (7.15) отражают зависимость х и s от скорости потока (D = F/V) в стационарном состоянии. Для очень медленных скоростей потока при заданном объеме, следовательно, s также приближается к нулю. Поскольку почти весь вводимый в реактор субстрат поглощается клетками, то концентрация клеточной массы на выходе из реакторах х будет равна S_fY_x/s.

По мере постепенного повышения D возрастает и s: сначала пропорционально D, а затем, по мере приближения D к µ_mах, еще быстрее. Точно таким же образом снижается и концентрация клеточной массы — сначала в линейной зависимости от D, а затем, при D→ µ_mах, с большей скоростью. При приближении D к µ_mах в какой-то момент х становится равной нулю; это означает, что скорость разведения D только что превысила максимально возможную скорость роста и решение уравнения (7.14) в условиях стационарного состояния возможно только при х = 0.

Потеря всех клеток в стационарном состоянии, называемая вымыванием, происходит, когда D больше D_mаx; последний параметр можно определить по уравнению (7.14) при х = 0:

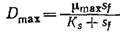
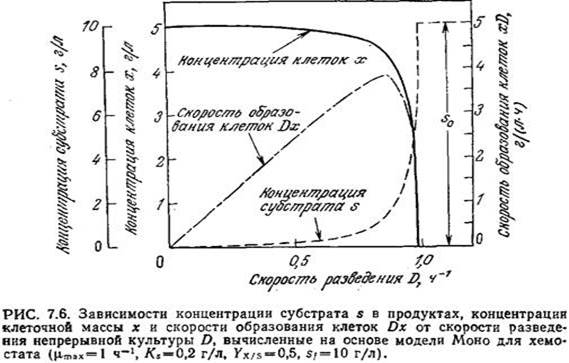
На рис. 7.6 приведены отражаемые уравнениями (7.14) и (7.15) графики зависимостей концентраций субстрата и клеточной массы от D для следующего ряда значений параметров:

µ_mах =1,0ч^-1 У_х/s = 0,5 Кs=0,2г/л s_f=10 г/л

Заметьте, что вблизи точки вымывания реакционная смесь становится очень чувствительной к колебаниям D; даже небольшое изменение D сопровождается относительно большим изменением х и (или) s.

Эту зависимость необходимо иметь в виду в тех случаях, когда целью непрерывного микробиологического процесса является производство биомассы. Скорость продуцирования клеток в единице объема реактора равна Dx; на кривой зависимости Dx от D (рис. 7.6) имеется резкий максимум. Максимальную скорость образования клеток можно вычислить, решив дифференциальное уравнение

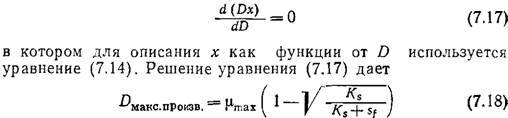
Если, как это часто бывает на практике, S_f>K_s, то D макс.произв. приближается к µ_mах и, следовательно, находится вблизи точки вымывания. В такой ситуации, изображенной, в частности, на рис. 7.6, как правило, чтобы избежать диапазона наибольшей чувствительности, целесообразно не добиваться максимальной скорости образования биомассы. Вообще при решении любых проблем оптимизации в поисках сравнительно легко регулируемых параметров важно не забывать практические аспекты сочетания чувствительности, регулируемости и надежности.

При изучении закономерностей образования конечных продуктов непрерывных микробиологических процессов введем еще один коэффициент Y_р/х, представляющий собой отношение

Вместе с приведенными выше уравнениями, выражающими зависимость |µ и х от параметров процесса, уравнение (7.21) позволяет вычислить концентрацию продукта в выходящем из реактора потоке. Производительность реактора по отношению к продукту равна pD и при постоянном Y_p/х максимальна, если D имеет значение, определяемое уравнением (7.18). Следовательно, при попытках добиться максимальной производительности процесса также необходимо учитывать фактор чувствительности. [При каком значении D величина pD максимальна, если Y_P/x = f (D) ?]

В качестве примера на рис. 7.7 приведены результаты экспериментального изучения роста культуры бактерий Aerobacter aerogenes в проточном реакторе. Экспериментальные результаты и описанная выше простая математическая модель качественно вполне согласуются. В то же время найденная скорость образования клеточной массы и найденная концентрация субстрата остаются приблизительно постоянными в значительно более широком диапазоне условий, чем следует из рассчитанных по уравнению Моно данных (рис. 7.6). Кроме того, модель Моно не согласуется с экспериментальными данными при очень низких и очень высоких скоростях разведения.

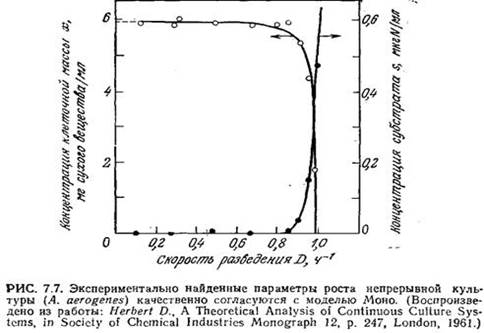В следующем разделе мы изучим эти две экстремальные ситуации и попытаемся понять, почему в таких случаях модель Моно неприменима.