Коэффициент Фехнера.
В статистической практике встречаются такие ситуации, когда значения факторных и результативных признаков не могут быть выражены численно. В этом случае для измерения тесноты зависимости необходимо использовать так называемые непараметрические методы.
Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируют не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.
Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.
Ранговый коэффициент корреляции Кендэла ( 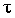 ) можно определить по формуле:
) можно определить по формуле:
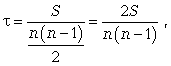
где S = P + Q.
Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП).
Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы (табл. 8.3).
Таблица 8.3
| Признаки | A | B | C | Итого |
| D | m11 | m12 | m13 | ∑m1j |
| E | m21 | m22 | m23 | ∑m2j |
| F | m31 | m32 | m33 | ∑m3j |
| Итого | ∑mj1 | ∑mj2 | ∑mj3 | П |
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.
Коэффициент взаимной сопряженности Пирсона определяется по формуле
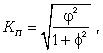
где 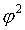 - показатель средней квадратической сопряженности:
- показатель средней квадратической сопряженности:
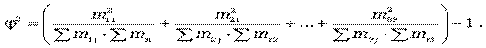
Коэффициент взаимной сопряженности изменяется от 0 до 1.
Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле
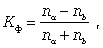
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической;
nb - соответственно количество несовпадений.
Коэффициент Фехнера может изменяться в пределах -1,0 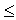 kф
kф 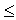 +1,0.
+1,0.
Дата добавления: 2016-07-18; просмотров: 2891;











