Виды средних показателей.

Средние величины- статистические показатели, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака.

Средняя величина отражает то, что характерно для единиц изучаемой совокупности. Они тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.

Средняя величина- обобщающий показатель, характеризующий уровень варьирующего признака в расчете на единицу однородной совокупно; в конкретных условиях места и времени.

Исчисление средних величин предполагает выполнение следующих требований:

1) качественная однородность совокупности, по которой исчислена средняя. Исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;

2) исключение влияния на исчисление средней величины случайных, сугубо индивидуальных причин и факторов. Достигается в том случае, когда исчисление средней основывается на массовом материале, в котором проявятся действие закона больших чисел и все случайности взаимно погашаются;

3) при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показатель (свойство), на который она должна быть ориентирована. Определяющий показатель может выступать в виде суммы значений осредняемого признака, сунны его обратных значений и т. п. Связь между определяющим показателем и средней выражается в следующем: если все значения осредняемого признака заменить их средним значением, то сумма или произведение в этом случае не изменит определяющего показателя.

Форма (формула) средней определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым. Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим. Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.

Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, - групповыми средними.Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.

Средние показатели иногда приводят к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.

С помощью метода средних решаются следующие задачи:

1) характеристика уровня развития явлений;

2) сравнение двух или нескольких уровней;

3) изучение взаимосвязей социально-экономических явлений;

4) анализ размещения социально-экономических явлений в пространстве.

Виды средних показателей

Средняя арифметическая(простая) применяется, когда общий объем варьирующего признака для всей совокупности образуется как сумма значений признаков у отдельных ее единиц. Ее вычисление сводится к суммирование всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности:

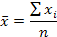
Средняя арифметическая(взвешенная) используется в тех случаях, когда известны отдельные значения признака и их веса (fi):

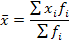
где хi—варианты осредняемого признака;

fi- частота, которая показывает, сколько раз встречается i-oe значение в совокупности.

В случае дискретного вариационного ряда для вычисления средней нужно значения вариантов умножить на соответствующие частоты и сумму этих произведений разделить на сумму частот.

Средняя хронологическаяприменяется для моментного ряда с равными интервалами между датам» (например, когда известны уровни на начало каждого месяца или квартала, года):

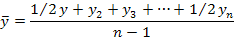
Средняя гармоническая (простая и взвешенная) применяется, когда характер исходных статистических данных таков, что расчет средней арифметической теряет смысл. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное отделения одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной:

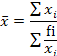
Средняя гармоническая(простая) применяется, когда веса всех вариантов (fi) равны:

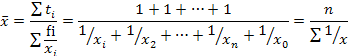
где хi. - отдельные варианты;

n – число вариантов осредняемого признака.

Средняя геометрическая(простая):

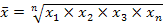
Средняя геометрическая(взвешенная):

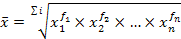
Средняя квадратическаяприменяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения иисчисляется по формулам:

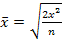(простая) 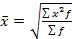(взвешенная)

Средняя кубическаяприменяется при расчете с величинами кубических функций и исчисляется по формуле:

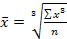(Простая) 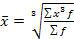(взвешенная)