Расчет простейших статистических неопределимых систем

Статически неопределимые системы (СНС) – системы, у которых число

неизвестных реакций связей превышает число независимых уравнений статики.

Таких уравнений статики для плоской системы – 3:

,

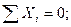
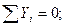
а для пространственной системы – 6:

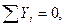
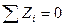
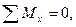
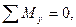
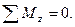
Следовательно, плоские СНС имеют число связей S > 3, а пространственные –

S > 6.

Примеры СНС даны на рис. 23. Стержень, жестко защемленный с двух сторон (“лишняя” связь – 1), (рис.23, а). Балка, имеющая жесткое защемление в сечении А и шарнирно – подвижная опора В (“лишняя” связь – 1), (рис.22 б). Рама, имеющая жесткое защемление в опоре А, и шарнирно-неподвижную опору В (“лишних” связей - 2). (рис.23 в).

Рис.23. Статистические неопределимые системы.

Для раскрытия статической неопределимости системы необходимо, прежде всего, определить степень статической неопределимости системы (n):

где n = S - УС

S – число связей, наложенных на систему.

УС – число независимых уравнений статики.

n - означает, сколько дополнительных уравнений деформаций необходимо составить, чтобы определить реакции, которые невозможно определить при помощи одних лишь уравнений статики.

При решении статически неопределенных систем используется метод сил. Метод сил заключается в том, что “лишние” связи, равные числу n, отбрасываются, а их действие заменяется неизвестными силами и моментами в зависимости от конструкции опорного закрепления. Неизвестные реактивные силы и моменты определяются посредством составления уравнений деформаций от этих сил моментов, заведомо зная, что они равны нулю. (Пример: задача 6-пр, стр.61)

Вопросы к 16

1. Что такое статически неопределимые системы?

2. Как определить степень статической неопределимости?

3. В чем заключается метод сечений?

4. Уравнение деформаций при раскрытии статической неопределимости.

5. Порядок решения СНС.

Тесты к 16

16.1. При решении СНС составляют уравнения:

а) статики: 3 для плоской системы, 6 для пространственной;

б) деформаций;

в) статики и деформаций, после чего эти уравнения решают совместно.

16.2. Степень статической неопределимости:

а) разность между числом связей и уравнений статики;

б) сумма числа связей и уравнений статики;

в) произведение числа связей и уравнений статики.

16.3. Метод сил:

а) определение и анализ внешних сил;

б) замена «лишних» связей силами и моментами;

в) определение внутренних сил методом сечений.

16.4. Уравнения статики:

а) 3 уравнения статики для плоской системы и 6 для пространственной;

б) уравнения моментов относительно опор;

в) число неизвестных сил.

16.5. Может ли быть статически неопределимым вал:

а) да;

б) нет;

в) только при нагружении сосредоточенными силами.

17. Примеры решения задач

Задача 1

Для заданной схемы нагружения стержня постоянного сечения (рис. 1-пр) F=5,0 кН

1) – построить эпюры внутренних сил;

- построить в общем виде эпюры напряжений;

- определить опасный участок;

- из условия прочности (s_max = [s]) = 120 МПа определить размер сечения;

- определить напряжения на участках стержня и построить эпюры напряжений стержня.

2) определить размеры равнопрочного стержня и экономию материала при равнопрочном стержне.

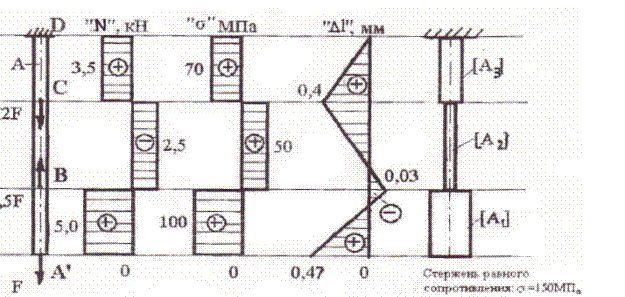
Рис.1-пр

Решение.

1. Разбиваем стержень на три участка: A׳B, BC, CD.

2. Определяем внутренние силы на каждом участке стержня.

N₁ = N_(AB) =F = 5,0 kH

N₂ = N_(BC) = F-1,5F = -2,5 kH

N₃ = N_(CD) = F-1,5F+1,2F = 0,7F = 3,5kH

3. Определяем напряжения на каждом участке.

s₍₁₎ =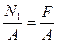

s_(II) =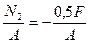

s_(III) =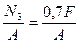

4. Определяем опасный участок.

Опасный участок АВ, где действует сила N₁=N_max=F=5,0 kH

5. Из условия прочности определим площадь сечения.

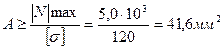
Принимаем А= 50 мм²

6. Определяем численные значения напряжений

s₍₁₎=

s₍₂₎=

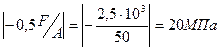
s₍₃₎=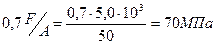

По полученным данным строим эпюру напряжений

7. Определяем перемещения на участках стержня

Е- модуль продольной упругости, Е= 2×10⁵ МПа (для стали)

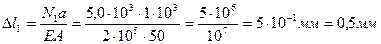
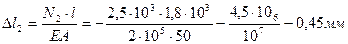
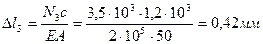
По полученным данным строим эпюру перемещений.

8. По полученным данным определяем размеры сечений равнопрочного стержня, у которого напряжения на каждом участке s_i=[s], i = 1,2,3.

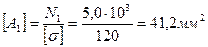
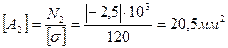
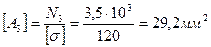
9. Определяем экономию материала в равнопрочном стержне.

Вес стержня с постоянным сечением, g - удельный вес.

Вес равнопрочного стержня.

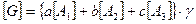
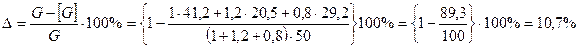
Задача 2

Для заданной схемы нагружения вала (рис. 2-пр)

- построить эпюры крутящих моментов;

- найти опасные сечения;

- определить диаметр вала из условия прочности;

- определить углы закручивания на участках вала, построить эпюру углов закручивания;

- проверить вал на жесткость, если [q]=1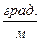

M=50 кHм, [t]=80МПа, а=1,0 м

Решение:

1. Разбиваем вал на участки: 1-й – АВ, 2-й – ВС, 3-й – СД.

Рассмотрим 1-й участок АВ

Проводим сечение 1-1 и рассмотрим равновесие отсеченной части и определяем крутящий момент в сечении 1-1

Мм₁ =М

Проводим сечение 2-2 и определяем крутящий момент в сечении 2-2. M_k2=M-3M=-2M

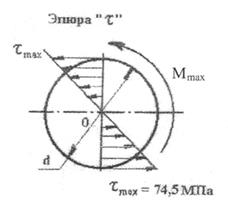рис. 2-пр

Крутящий момент в сечении 3-3

M_k3=M-3M+1,5M=-0,5M

По полученным данным строим эпюру “M_k”

2. Определяем опасное сечение. Опасными сечениями являются все сечения участка 2, где M_max= [M_k] = 2M=100 kHм

3.Определяем диаметр вала из условия прочности

Откуда полярный момент сопротивления

=

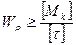
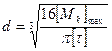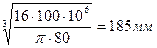
Принимаем d=190 мм

;

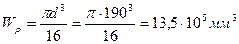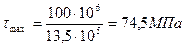
4.Определяем углы закручивания на участках вала

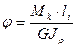, где:

l_i – длина участка : a; 1,5а; 0,8а

G – модуль упругости при сдвиге

G= 0,8 × 10⁵ МПа

J_r - полярный момент инерции вала

J_r =

угол закручивания на участке 3:

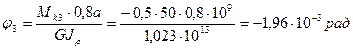
угол закручивания на 2-ом участке:

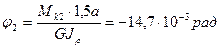
угол закручивания на 1-ом участке:

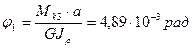
5.Определяем относительные углы закручивания

Q₁=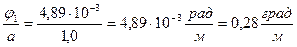

Q₁<[Q]; 0,28<1

Q₂=

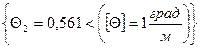
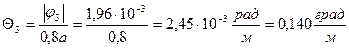
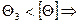условие жесткости выполняется

6.Определим диаметр вала из условия прочности

Округляем диаметр d = 130 мм.

Применяем диаметр вала d=190мм, удовлетворяющий условиям прочности и жесткости

Задача 3

При заданной схеме нагружения стальной балки двутаврового сечения (рис. 3-пр)

- построить эпюры Q(x) и M(x)

- определить величины заданных внешних нагрузок q, F и M.

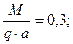
Дано: 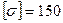МПа; 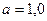м; двутавр №18

Решение:

1. Определяем опорные реакции

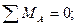
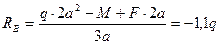
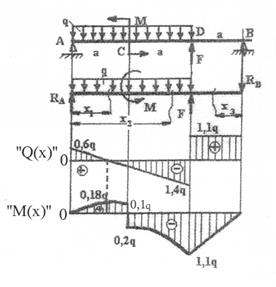Рис. 3-пр

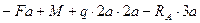
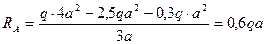
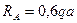=0,6а

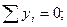
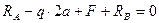
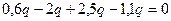
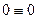
2. Разбиваем балку О на 3 участка (АС; СD; DB)

Участок АС(0 £ x₁ £ a)

Q_(x1) = R_A - q× x₁; M(x₁) = R_A × x₁ – q× x₁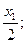

x₁=0; Q(0) = R_A = 0,6q x₁=0; M(0) = 0

x₁=a; Q(a) = R_A – qa = 0,6q-q =-0,4q x₁=a; M(a) = 0,6q× 1-q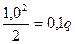

Находим М_max. R_A - q 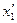=0;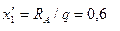

M(x₁)_max=0,6q× 0,6 -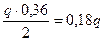

Участок CD (a £ x₂ £ 2a)

=

=

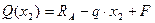
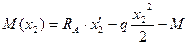
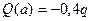
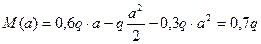
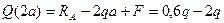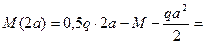
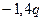
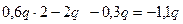
Участок DB (0 £ x₃ £a)

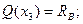
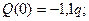
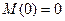
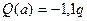
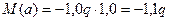
По полученным результатам строим эпюры Q и M. В точке d эпюры изгибающих моментов.

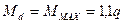, - это опасное сечение (при а=1м).

По заданной величине допустимого напряжения [s] = 150 МПа определяем величины предельных нагрузок.

Для двутавра №18 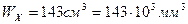(по таблицам сортамента)

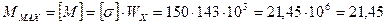kH×м

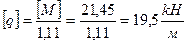
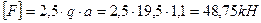
Задача 4

Для заданной схемы нагружения стержня, у которого:

l = 6м; F = 700kH ; [s] = 160МПа; ( рис.-4-пр)

Найти: а, F_кр

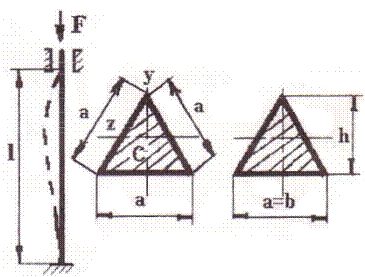
Рис.4-пр

Решение:

1. Определяем осевые моменты инерции:

;

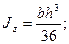
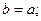
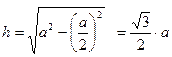
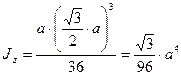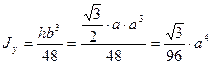
2.Определяем радиус инерции сечения: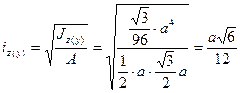

Площадь сечения: 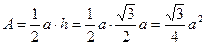=0,433а²

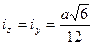=0,204а

3.Определяем размер сечения из условий устойчивости:

- Первое приближение: принимаем j_о = 0,5

Площадь сечения: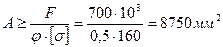

Сторона сечения: ;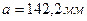

Радиус инерции сечения:

Гибкость стержня:

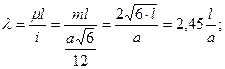
m- коэффициент приведенной длины стержня; m = = 0,5

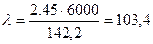
По таблице 1.13, Дарков и Шпиро, “Сопротивление материалов”

- j = f(l); j₁= 0,58

- Второе приближение: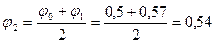

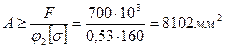; 136 мм

;

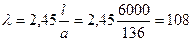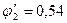
Следовательно, при а=136 мм стержень удовлетворяет условию устойчивости.

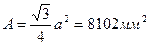
- Определяем критическую силу:

Определяем коэффициент запаса по устойчивости:

Задача 5

Для заданной схемы нагружения вала определить его диаметр из условия прочности (рис.5-пр):

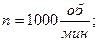Т₁ и Т₂ –силы напряжения ремней шкивов

Диаметры шкивов:

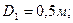
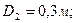
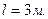
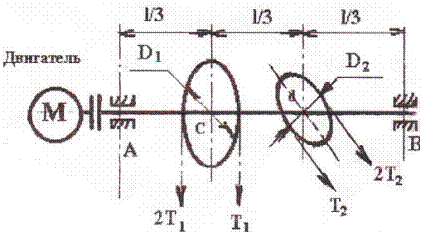
Рис. 5-пр

;

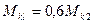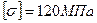
Найти: d- диаметр вала по III^й теории прочности

Решение:

1. Крутящий момент от электродвигателя:

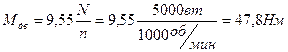
2. Определяем крутящий момент на участках вала:

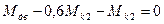
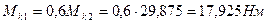
3. Определяем усилия в ремнях шкивов.

1-й шкив:

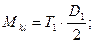
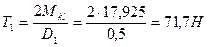
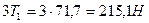
2-й шкив:

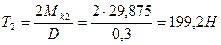
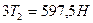
4. Строим эпюры крутящих моментов и изгибающих моментов в горизонтальной и вертикальной плоскостях (5.1-пр.).

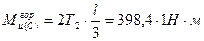
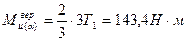
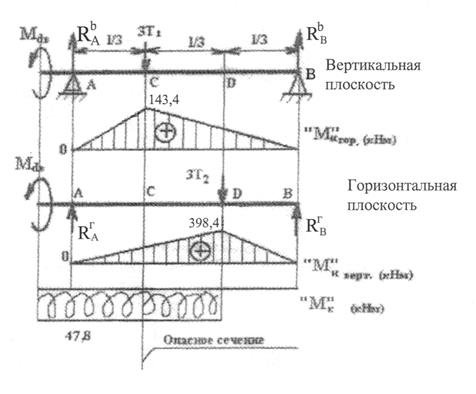
Рис. 5.1-пр.

5. Определяем приведенный момент по III теории прочности в опасном сечении.

Опасным сечение является сечение С, где:

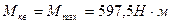
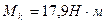
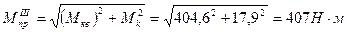
Определяем диаметр вала:

7.

d=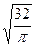

Принимаем диаметр d = 40мм.

Задача 6.

Для заданной схемы нагружения статически неопределимой системы (6-пр).

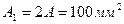
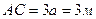
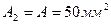
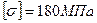
1. Найти: R_E и R_A

2. Построить эпюры: N; s; Dl.

Решение:

1. Отбрасываем опору Е и заменяем ее действие реакцией R_E

2. Разбиваем стержень на участки (1-й – de, 2-й – cd, 3-й – cd, 4-й – ba) и определяем внутренние силы на каждом участке

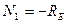
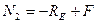
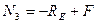
3. Составляем уравнение статики

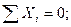
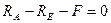(1)

4. Составляем уравнение деформаций

(2)

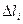- деформация на i – том участке

i = 1,2,3,4

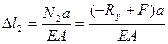
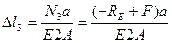(3)

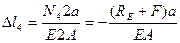
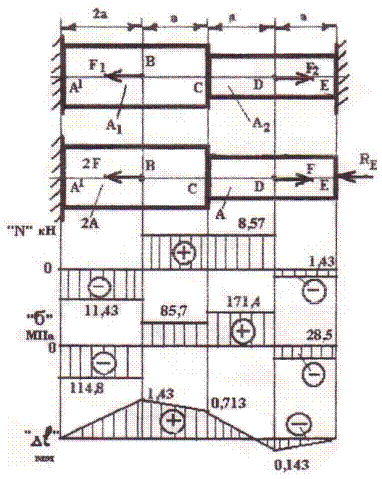
рис. 6-пр

5. Значения (3) подставляем в уравнение (2)

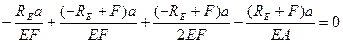
Сокращаем на ЕА и а

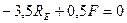
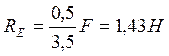
6. Подставляем R_E в уравнение (1) и определяем R_A

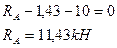
7. Определяем внутренние силы на участках стержня

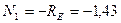kH

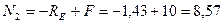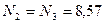kH

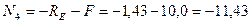kH

kH

8. Определяем напряжения на участках стержня

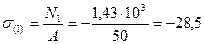МПа

МПа

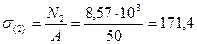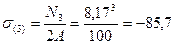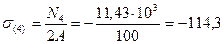МПа

МПа

9. Определяем перемещения на участках стержня

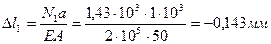
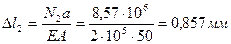
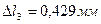
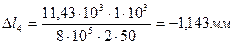
Проверка:

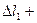
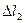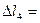+ + 0 ∑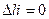

-0,143 + 0,857 + 0,429 -1,143 = 0

0=0

Задача решена верно.

Задача 7

В опасном поперечном сечении вала, ослабленном шпоночной канавкой, возникает крутящий момент М_к = 370 Н × м, изменяющийся по пульсационному циклу и изгибающий момент М_u = 380 Н × м, изменяющийся по симметричному циклу (7-пр). Определить коэффициент запаса прочности n, для опасного сечения, сравнить с величиной допустимого коэффициента запаса [ 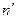] =1,8

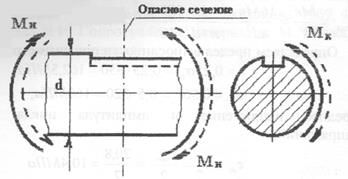
Рис. 7-пр

Диаметр вала d = 45мм

Материал вала – углеродистая сталь с механическими характеристиками:

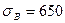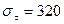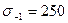МПа; МПа; МПа

Принимаются [7]

К_s = 1,95; b _Мs = 1,33; b _ns = 1,07;

К_t = 1,80; b _Мt = 1,33; b _nt = 1,04

Решение:

1. Определяем коэффициент запаса прочности по нормальным и касательным напряжениям отдельно:

По нормальным напряжениям: 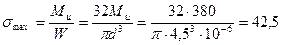МПа

Так как:

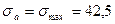МПа;

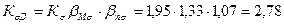
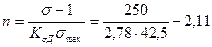
Коэффициент запаса по текучести: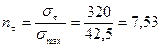

Принимаем меньшее значение коэффициента: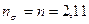

По касательным напряжениям: 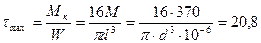МПа

2. Определяем предел выносливости при симметричном цикле:

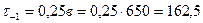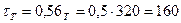МПа; МПа

Среднее напряжение и амплитуда цикла касательных напряжений:

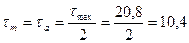МПа

3. Определяем коэффициент запаса по усталостному разрушению:

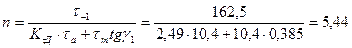
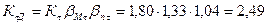и

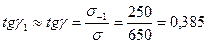
Коэффициент запаса текучести:

Принимаем меньшее значение запаса: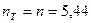

4. Окончательное значение коэффициента запаса:

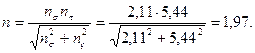n>[n] 1,97>1,8

Запас прочности обеспечен .