Уравнения в частных производных

Уравнение

F(х₁, х₂,..., х_m, u, 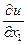,..., , 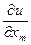, ,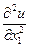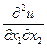...) = 0,

связывающее неизвестную функцию u(х₁, х₂,..., х_m), независимые переменные х₁, х₂,..., х_m и частные производные неизвестной функции, называется уравнением в частных производных. Порядок п старшей производной называется порядком дифференциального уравнения.

Уравнение в частных производных называется линейным, если оно линейно относительно неизвестной функции и её частных производных.

Приведем основные уравнения математической физики, которые являются линейными уравнениями в частных производных второго порядка.

1. Волновое уравнение (уравнение колебаний)

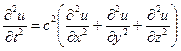(8.1)

описывает различные виды волн – звуковые, упругие, электромагнитные и другие колебательные процессы. Функция u = u(х, у, z, t) зависит от пространственных переменных х, у, z и времени t.

2. Процесс распространения тепла в однородном изотропном теле

описывается уравнением теплопроводности

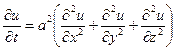(8.2)

Уравнение теплопроводности в общем виде записывается так:

c(х, у, z, t) = div[k(u, х, у, z, t) grad u] + q(х, у, z, t),

grad u = ,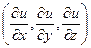

div(X(x, y, z), Y(x, y, z), Z(x, y, z)) =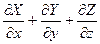

Здесь u = u(х, у, z, t) – температура в точке (х, у, z) в момент времени t,

c(u, х, у, z, t) – теплоемкость в точке (х, у, z) в момент времени t, k(u, х, у, z, t) – коэффициент теплопроводности в точке (х, у, z) в момент времени t,

q(u, х, у, z, t) – плотность источников тепла.

3. Установившееся тепловое состояние в однородном изотропном теле

описывается уравнением Пуассона

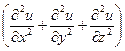= -f(x, y, z). (8.3)

Установившееся тепловое состояние в однородном изотропном теле при отсутствии источников тепла внутри тела описывается уравнением Лапласа

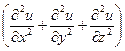= 0. (8.4)

В уравнениях (8.3) и (8.4) функция u = и(х, у, z) зависит только от пространственных переменных х, у, z.

Согласно классификации уравнений второго порядка уравнение (8.1) относится к гиперболическому типу, (8.2) – к параболическому типу, а (8.3), (8.4) – к эллиптическому типу.

В конкретной постановке задачи математической физики необходимо найти решение одного из уравнений (8.1) – (8.4), удовлетворяющее дополнительным (начальным и граничным) условиям.

Начальные условия задаются с уравнениями (8.1), (8.2) и обычно имеют вид

u(x, y, z, t₀) = u₀(x, y, z), (8.5)

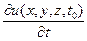= u₁(x, y, z). (8.6)

При этом для уравнения (8.1) искомое решение u = u(х, у, z, t) должно удовлетворять в начальный момент времени t₀ условиям (8.5) и (8.6), а для уравнения (8.2) – одному из условий (8.5), (8.6).

Граничные условия для уравнений (8.1), (8.2): искомое решение

u = u(х, у, z, t) должно удовлетворять на границе тела (или среды) одному из условий

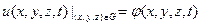, (8.7)

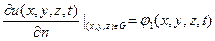, (8.8)

где 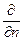– производная по направлению нормали к границе G тела.

Для уравнений Пуассона или Лапласа задаются только граничные условия

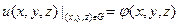(8.9)

или

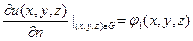(8.10)

Задача для уравнения Лапласа (8.5) с граничным условием (8.9) называется задачей Дирихле, а с условием (8.10) – задачей Неймана.

Область Ω, описывающая тело, может быть задана в трехмерном, двумерном или одномерном пространствах. В первом случае функция u = u(х, у, z, t) зависит от трех пространственных переменных (х, у, z) и времени t, во втором – от двух пространственных переменных (х, у) и времени t: u = u(х, у, t), а в третьем случае – от переменных х и t: и = и(х, t).

Рассмотрим разностный метод решения задач для уравнений в частных производных, который описывается ниже на примерах основных задач математической физики.

8.1. Разностный метод для уравнения колебаний

а) Уравнение колебаний струны. Явная схема

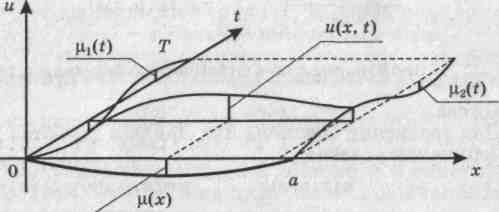
Рассмотрим задачу о малых колебаниях натянутой струны с распределенной по длине нагрузкой f(x, t) (рис. 8.1):

u_tt = c²u_xx + f(x, t), 0 < x < a, 0 < t < T, (8.11)

u(x, 0) = μ(x), u_t(x, 0) = μ₀(x), 0 < x < a, (8.12)

u(0, t) = μ₁(t), u₂(a, t) = μ₂(t), 0 £ t £ T. (8.13)

Рис. 8.1

Струна совершает плоскиеколебания, т. е. точки струны перемещаются параллельно плоскости t = 0.

Функция u(х, t) выражает смещение точки х струны в момент времени t от прямолинейной формы.

Начальные условия (8.12) означают следующее. Форма струны в начальный момент времени t = 0 выражается функцией μ(x). Скорость перемещения точки х струны в момент времени t = 0 равна значению функции μ₀(х).

Краевые условия (8.13) говорят о том, что левый конец струны с течением времени совершает смещение μ₁(t), a правый конец – смещение μ₂(t).

Если концы струны закреплены, то μ₁(t) = μ₂(t) = 0.

При этом предполагается, что начальные условия (8.12) и краевые условия (8.13) должны быть согласованы между собой в угловых точках, т. е. выполнены условия u(0, 0) = μ(0) = μ₁(0), u(а, 0) = μ(a) = μ₂(a).

На рис. 8.1 представлен случай, когда

u(0, 0) = μ(0) = μ₁(0) = 0, u(а, 0) = μ(a) = μ₂(a) = 0.

Введем сеточную область (рис. 8.2, а). В прямоугольной области 0 £ x £ a,

0 £ t £ T зададим точки

(x_i, t_k), x_i= ih, i = l,..., N;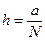

t_k = kτ, k = 0, 1, ... , M; τ = 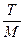(8.14)

Рассмотрим уравнение (8.11) в точках (x_i, t_k), i = 1,..., N - 1, k = 1,..., М - 1, и заменим производные разностными формулами

u_tt(x_i, t_k)=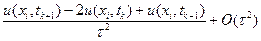

(8.15)

u_xx(x_i, t_k)=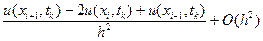

Обозначим через u_i_,_k приближенные значения искомой (функции в точках (x_i, t_k). Тогда из уравнения (8.11) получим разностное уравнение (разностную схему), которое аппроксимирует уравнение (8.11) с порядком О(h² + τ²):

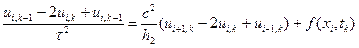
(8.16)

i = 1,..., N - 1; k = 1,..., M - 1.

На рис. 8.2, б изображен шаблон «крест» разностного уравнения (8.16). Разностное уравнение (8.16) связывает значения неизвестной функции на трех слоях (k – 1, k, k + 1)

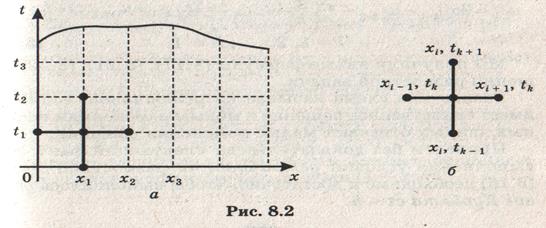
На слое k = 0 заданы начальные условия (8.12), из которых следует, что

u_i_, ₀ = μ(x_i), i = 1, 2, ... , N - 1. (8.17)

Чтобы найти значения неизвестной функции на слое k = 1, используем условие для производной u_t(x, 0) из (8.12). Для этого построим разложение в ряд Тейлора:

u(x_i, t₁) = u(x_i, τ) = u(x_i, 0) + u_t(х_i, 0)τ + 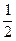u_tt(x_i, 0)τ²+ O(τ³). (8.18)

Из уравнения (8.11), учитывая первое условие в (8.12), выразим вторую производную

u_tt(x_i, 0) = c²u_xx(x_i, 0) + f(x_i, 0) = с²μ''(х_i) + f(х_i, 0). (8.19)

Теперь, учитывая условие u_t(x, 0) = μ₀(x) в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое:

u(x_i, t₁) = μ(x_i) + μ₀(x_i)τ + 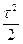(с²μ''(х_i) + f(х_i, 0)) + О(τ³). (8.20)

С учетом (8.13) окончательно получим для приближенных значений искомой функции на первом слое формулы

u_i_, ₁ = μ(x_i) + μ₀(x_i)τ +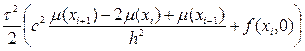

i = 1, 2,..., N - 1; u_0, ₁ = μ₁(t₁), u_N_, ₁ = μ₂(t₁). (8.21)

Учитывая граничные условия (8.13), из (8.16) выводим формулы для вычисления значений на слоях k = 2,..., М:

u_0, _k = μ₁(t_k), u_N_, _k = μ₂(t_k).

u_i_, _k = 2u_i_, _k _- ₁ - u_i_, _k _- ₂ +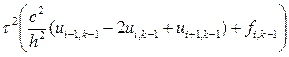

i = 1, 2,..., N - 1. (8.22)

Таким образом, получены явные формулы (8.17), (8.21), (8.22) решения разностной задачи.

Разностная схема называется устойчивой, если она имеет единственное решение и малым изменениям исходных данных отвечают малые изменения решения.

Известен следующий факт: для выполнения условия устойчивости разностной схемы (8.16) необходимо и достаточно, чтобы выполнялось условие Куранта сτ < h.

Говорят, что решение разностной схемы (8.16) сходится к решению исходной задачи (8.11) – (8.13), если выполняется условие

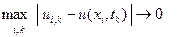при h ® 0 и τ ® 0.

Если разностная схема устойчива и аппроксимирует исходную задачу, решение разностной схемы сходится к решению задачи.

Сформулируем алгоритм решения задачи о колебаниях струны (8.11) –(8.13) с помощью явной разностной схемы (8.16).

1. Построить сеточную область

(x_i, t_k), x_i= ih, i = 0, l,..., N;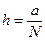

t_k = kτ, k = 0, 1, ... , M; τ =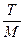

выбирая шаги h и τ так, чтобы выполнялось условие устойчивости (условие Куранта) сτ < h.

2. Вычислить значения u_i_,_k искомой функции для k = 0,1:

u_i_, ₀ = μ(x_i), i = 0, 1, ... , N,

u_i_, ₁ = μ(x_i) + μ₀(x_i)τ +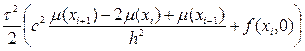

i = 1,..., N - 1; u_0, ₁ = μ₁(t₁), u_N_, ₁ = μ₂(t₁). (8.23)

3. Вычислить значения u_i_,_k для k = 2,..., M:

u_0, _k = μ₁(t_k), u_N_, _k = μ₂(t_k).

u_i_, _k = 2u_i_, _k _- ₁ - u_i_, _k _- ₂ +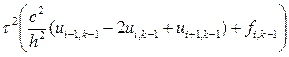

i = 1, 2,..., N - 1. (8.24)

б) Уравнение колебаний струны. Неявная схема

Построим неявную схему для уравнения колебаний струны (8.11):

=

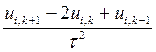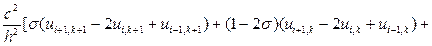
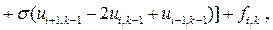(8.25)

i = 1,..., N – 1; k = 1,..., M; .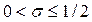

Для устойчивости схемы (8.25) параметры с, h, τ, σ должны удовлетворять условию:

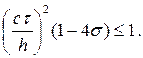
Если 1/4 £ σ £ 1/2, схема (8.25) безусловно устойчива.

Шаблон схемы (8.25) изображен на рис. 8.4

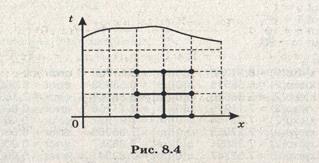
Значения решения на нулевом и первом слоях вычисляют по формулам (8.23). На каждом k-м слое (k = 2, 3, ... , М) решают методом прогонки систему уравнений относительно u_i_,_k₊₁i = 1, 2, ... , N - 1:

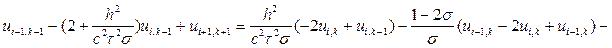
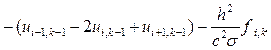(8.26)

Алгоритм решения неявной разностной схемы для уравнения колебаний струны:

0. Построить сеточную область, выбирая шаги h, τ и параметр σ так, чтобы выполнялось условие устойчивости

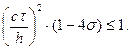
Если 1/4 £ σ £ 1/2, можно выбирать h, τ произвольно.

1. Вычислить значения u_i_,_k искомой функции для k = 0, 1:

u_i_,0= μ(x_i), i = 0, 1,..., N; (8.27)

u_i_,1 = μ(x_i) + μ₀(x_i)τ + 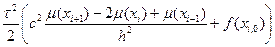, (8.28)

i = 1,..., N – 1; u_0, ₁ = μ₁(t₁), u_N_, ₁ = μ₂(t₂)

2. Значения u_i_,_k₊₁ для каждого k > 0 находим методом прогонки.

2.1. Вычислим правые части (8.26):

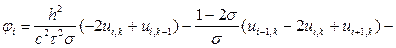
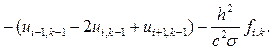(8.29)

i = 1,..., N – 1.

2.2. Вычислим прогоночные коэффициенты;

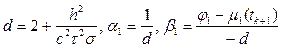(8.30)

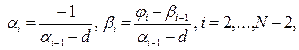(8.31)

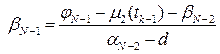. (8.32)

2.3. Вычислим решение u_i_,_k₊₁:

u_{0, k + 1} = μ₁(t_k_{+ 1}), u_N_{, k + 1} = μ₂(t_k_{+ 1}),

u_N_{– 1, k + 1} = β_N_{– 1}, (8.33)

u_i_{, k + 1} = α_iu_i_{+ 1, k + 1} + β_i,

i = N – 2, N – 3,..., 1. (8.34)

8.2. Разностный метод для уравнения колебаний мембраны

Рассмотрим задачу для уравнения колебаний однородной прямоугольной мембраны:

u_tt = c²(u_xx + u_yy) + f(x, у, t), (8.35)

0 < x < a, 0 < y < b, 0 < t < T.

u(x, у, 0) = μ(x, у), 0 < х < a, 0 < у < b. (8.36)

u_t(x, у, 0) = μ₀(x, у), 0 < х < a, 0 < у < b. (8.37)

u(0, у, t) = μ₁(y, t), u(a, у, t) = μ₂(y, t)

0 £ y < b, 0 £ t £ T.

u(x, 0, t) = μ₃(x, t), u(x, b, t) = μ₄(x, t) (8.38)

0 £ x < a, 0 £ t £ T.

Введем сеточную область:

(x_i, y_j, t_k), x_i = ih_x, i = 0, ..., N_x, h_x = ,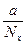

y_j = jh_y, j = 0, ..., N_y, h_y = ,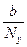

t_k = kτ, k = 0, ..., M, τ = .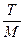

Обозначим u_i,j,k = u(x_i, у_j, t_k). Заменяя производные Разностными формулами для уравнения (8.35), получим разностное уравнение с порядком аппроксимации O( ):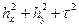

+

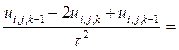
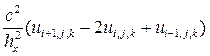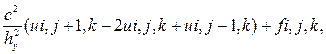+ (8.39)

i = 1, ..., N_x – 1, j = 1, ..., N_y – 1, k = 1, ..., M – 1.

Таким образом, получена явная разностная схема, аналогичная явной схеме для уравнения колебаний струны.

<== предыдущая лекция	\|	следующая лекция ==>
Численные методы решения обыкновенных дифференциальных уравнений	\|	Вероятностные методы. Метод Монте-Карло

Дата добавления: 2020-08-31; просмотров: 502;