Математическая модель и погрешности
Процесс решения задачи из физики, техники или экономики с помощью методов математического моделирования можно представить на следующей схеме:

1. На первом этапе проводится исследование объектаи формулируется содержательная(физическая, техническая, экономическая и др.) постановка задачи. Для того чтобы задачу можно было описать количественно, нужно провести качественный и количественный анализ свойств объекта и выделить основные параметры, оказывающие на них наиболее существенное влияние.
2. Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической моделиобъекта. Под математической моделью понимают систему математических соотношений (уравнений, неравенств, краевых, начальных условий), которым должна удовлетворять система основных параметров задачи или объекта. Одно из основных требований, предъявляемых к математической модели, – соответствие исследуемому объекту, т. е. адекватность.Другое немаловажное требование – чтобы модель была не слишком сложной, доступной для математической обработки. Умение находить оптимальное сочетание адекватности и сложности зависит от квалификации и даже интуиции исследователя и является в определенной степени искусством.
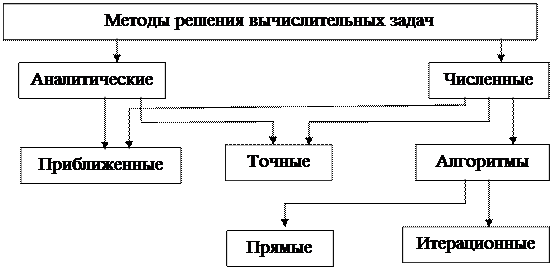
3. На следующем этапе необходимо найти методы (алгоритмы) решения математической задачи. В некоторых, наиболее простых случаях удается построить аналитическое решениезадачи. Такие решения являются наиболее привлекательными, поскольку позволяют не только количественно, но и, что не менее важно, качественно проанализировать исследуемые параметры. К сожалению, в подавляющем большинстве случаев это не представляется возможным, и для решения математической задачи применяются численные методы. Как аналитические, так и численные методы решения задач подразделяются на точные иприближенные.
К точным относят такие методы, которые позволяют получить решение задачи с любой, заранее заданной точностью.
Приближенные методы не предоставляют такой возможности. В этих
случаях при построении решения должна быть произведена оценка погрешности, или остаточного члена. В свою очередь, численные методы решения задач разбиваются на 2 группы.
К первой относятся так называемые прямые методы- алгоритмы, позволяющие за конечное, заранее определенное число арифметических действий получить решение задачи.
Вторую группу составляют методы последовательных приближений, или так называемые итерационные методы.
На следующей схеме приведена классификация методов решения вычислительных задач.
 |
4. Четвертым этапом является разработка программы решения задачина компьютере, ее тестирование и отладка. Может оказаться так, что рассматриваемая математическая задача исследована, и для ее решения разработаны стандартные программы, которые могут существовать отдельно или входить в пакеты прикладных программ. Тогда остается только выбрать подходящую программу или пакет прикладных программ.
5. На заключительном этапе выполняют вычислительные экспериментына компьютере и проводят анализ результатов. Если результаты не удовлетворяют исследователя, требуется совершенствование алгоритма или метода решения задачи, ее математической модели, а в некоторых случаях – корректировка содержательной постановки.
1.2. Источники и классификация погрешностей
Выделим следующие основные источники погрешностей:
а) параметры, входящие в описание задачи, заданы неточно; соответствующую погрешность называют неустранимой;
б) математическая модель описывает изучаемый объект приближенно с учетом основных, наиболее существенных факторов (погрешность математической модели);
в) численный алгоритм, применяемый для решения математической задачи, зачастую дает лишь приближенное решение (погрешность метода);
г) в процессе вычислений на компьютере промежуточные и конечные результаты округляются (вычислительная погрешность или погрешность округления).Методы, причисляемые к точным, не учитывают наличие вычислительной погрешности.
Часто первые два вида погрешности, объединяя в один, также называют неустранимой погрешностью.
Обозначив через I абсолютную величину погрешности результата, а через IН, IМи IО– абсолютные величины неустранимой погрешности, погрешности метода и округления соответственно – нетрудно получить следующее соотношение:
I ≤ IН + IМ + IО. (1.1)
Неравенство (1.1) дает оценку для погрешности результата. Из этого неравенства можно сделать важный вывод: полную погрешность результата нельзя сделать меньше, чем наибольшая из составляющих ее погрешностей.
1.3. Элементы теории погрешностей
Определение 1.1. Приближенным значениемнекоторой величины а называется число ар, которое незначительно отличается от точного значения этой величины.
Пусть а – точное значение некоторой величины, а ар – ее приближенное значение.
Определение 1.2. Абсолютной погрешностьюΔ приближенного значения называется модуль разности между точным и приближенным значениями этой величины:
Δ = | а - ар|.(1.2)
Определение 1.3. Относительной погрешностью приближенной величины ар называется отношение абсолютной погрешностиприближенной величины к абсолютной величине ее точного значения:
δ = 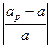 =
= 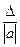 . (1.3)
. (1.3)
Это равенство можно записать в другой форме:
Δ = |а|× δ. (1.4)
На практике, как правило, точное значение величины неизвестно. Поэтому вместо теоретических понятий абсолютной и относительной погрешностей используют практические понятия предельной абсолютной погрешностии предельной относительной погрешности.
Определение 1.4. Под предельной абсолютной погрешностьюприближенного числа понимается всякое число Δa, не меньшее абсолютной погрешности этого числа:
Δ = | а - ар| ≤ Δа. (1.5)
Неравенство (5) позволяет для точного значения величины получить оценку
ар - Δа ≤ а ≤ ар + Δа. (1.6)
Часто неравенства (6) записывают в другой форме
а = ар ± Δа = ар (1 ± Δа). (1.7)
На практике в качестве предельной абсолютной погрешности выбирают наименьшее из чисел Δа, удовлетворяющих неравенству (1.5), однако это не всегда возможно.
Определение 1.5. Предельной относительной погрешностью δа данного приближенного числа называется любое число, не меньшее относительной погрешности этого числа:
δ ≤ δа. (1.8)
Так как справедливо неравенство
δ = 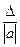 ≤
≤ 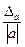 ,
,
то можно считать, что предельные абсолютная и относительная погрешности связаны формулой
δа = 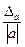 или Δа = |а| × δа. (1.9)
или Δа = |а| × δа. (1.9)
Если абсолютная погрешность Δа значительно меньше точного значения |а|,то относительную погрешность определяют приближенно как отношение абсолютной погрешности к приближенному значению:
δа » 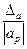 , Δа » |аp| × δа. (1.10)
, Δа » |аp| × δа. (1.10)
Часто в формуле (1.10) вместо знака «»» используют знак точного равенства « = ».
Относительную погрешность иногда задают в процентах.
1.4. Значащие цифры
Определение 1.6. Значащими цифрами в записи приближенного числа называются все цифры в его записи, начиная с первой ненулевой слева.
Определение 1.7. Первые п значащих цифр в записи приближенного числа называются верными в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего п-йзначащей цифре, считая слева направо.
Наряду с данным определением иногда используется другое.
Определение 1.8. Первые п значащих цифр в записи приближенного числа называются верными в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего n-йзначащей цифре.
1.5. Правило округления чисел
Чтобы округлить число до п значащих цифр, отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом:
1) если первая отброшенная цифра меньше 5, то оставшиеся десятичные знаки сохраняют без изменения;
2) если первая отброшенная цифра больше 5, то к последней оставшейся цифре прибавляют единицу;
3) если первая отброшенная цифра равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляют единицу;
4) если первая из отброшенных цифр равна 5 и все отброшенные цифры являются нулями, то последняя оставшаяся цифра оставляется неизменной, если она четная, и увеличивается на единицу, если нет (правило четной цифры).
Это правило гарантирует, что сохраненные значащие цифры числа являются верными в узком смысле, т. е. погрешность округления не превосходит половины разряда, соответствующего последней оставленной значащей цифре. Правило четной цифры должно обеспечить компенсацию знаков ошибок.
Следующая теорема выявляет связь относительной погрешности числа с числом верных десятичных знаков.
Теорема 1.1. Если положительное приближенное число имеет п верных значащих цифр, то его относительная погрешность δ не превосходит величины 101 - n, деленной на первую значащую цифру ан:
δ ≤ 101 - n / ан. (1.11)
Формула (11) позволяет вычислить предельную относительную погрешность
δa = 101 - n / ан. (1.12)
1.6. Погрешности арифметических операций
Приведем правила вычисления погрешности результата различных арифметических операций над приближенными числами.
Относительно алгебраической суммы u = х ± у можно утверждать следующее.
Теорема 1.2. Предельная абсолютная погрешность суммы приближенных чисел равна сумме предельных абсолютных погрешностей слагаемых, т. е.
Δu = Δx + Δy. (1.13)
Из формулы (1.13) следует, что предельная абсолютная погрешность суммы не может быть меньше предельной абсолютной погрешности наименее точного из слагаемых, т. е. если в состав суммы входят приближенные слагаемые с разными абсолютными погрешностями, то сохранять лишние значащие цифры в более точных не имеет смысла.
Теорема 1.3. Если все слагаемые в сумме имеют один и тот же знак, то предельная относительная погрешность суммы не превышает наибольшей из предельных относительных погрешностей слагаемых:
δu ≤ 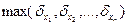 . (1.14)
. (1.14)
При вычислении разности двух приближенных чисел и = х - у её абсолютная погрешность, согласно теореме 2, равна сумме абсолютных погрешностей уменьшаемого и вычитаемого, т. е. Δu = Δx + Δy, а предельная относительная погрешность
δu = 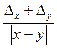 .(1.15)
.(1.15)
Из формулы (1.15) следует, что если приближенные значения х и у близки, то предельная относительная погрешность будет очень большой.
В некоторых случаях удается избежать вычисления разности близких чисел с помощью преобразования выражения так, чтобы разность была исключена.
Если представляется сложным заменить вычитание близких приближенных чисел сложением, то следует поступать так: если известно, что при вычитании должно пропасть m первых значащих цифр, а в результате требуется сохранить п верных цифр, тогда в уменьшаемом и вычитаемом следует сохранять m + п верных значащих цифр.
Теорема 1.4. Предельная относительная погрешность произведения и = х× у приближенных чисел, отличных от пуля, равна сумме предельных относительных погрешностей сомножителей, т. е.
δu = δx + δy. (1.16)
В частности, если и = kx, где k – точное число, имеем Δu = |k|Δx, δи = δх.
Теорема 1.5. Предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя.
1.7. Погрешность произвольной функции
Пусть задана произвольная функция и = f(xl, x2,..., хn), где xl, х2,…, хп – приближенные величины, а 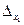 ,
, 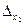 ,…,
,…, 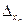 – их известные предельные абсолютные погрешности. Тогда предельная абсолютная погрешность результата – функции и – для малых
– их известные предельные абсолютные погрешности. Тогда предельная абсолютная погрешность результата – функции и – для малых 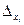 , вычисляется по формуле
, вычисляется по формуле
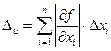 (1.17)
(1.17)
Как видно из формулы (1.17), для ее применения требуется, чтобы функция f(xl, x2,..., хn)была дифференцируемой по всем переменным.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Алгебраические и трансцендентные уравнения |
Дата добавления: 2020-08-31; просмотров: 1465;











