Отношение предпочтения и функция полезности

В отличие от предыдущего, второй подход не требует измерения полезности в каком-либо количестве. Потребитель здесь может сравнить полезность отдельных товаров или их набора и упорядочить их по степени предпочтения. Теория оптимального выбора потребителя исходит из того, что он осуществляет право сравнения и свободного выбора на некотором множестве X потребительских наборов, в каждый из которых включаются все виды продукции, являющиеся предметами потребления для данной группы семей. Не умаляя общности, можно считать, что всякий такой набор состоит из фиксированного числа ( n ) элементов и имеет вид:

x = (x₁, . . . , x_j, . . . , x_n) ,

где элементы x_j ³ 0 , поскольку они выражают количество потребляемой продукции.

Далее предполагается, что сравнительная оценка различных наборов данным потребителем с точки зрения его вкусов, привычек, традиций и т.д., может быть выражена при помощи т.н. бинарного отношения слабого предпочтения.

Это отношение определено на множестве потребительских наборов X , выражается формулой «предпочтительнее чем ...или равноценен», записывается при помощи знака «= « .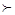

Формула «x= 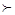y» , где x и y суть потребительские наборы означает, что данный потребитель (группа семей) в равных условиях либо предпочтет набор x набору y, либо не видит различия между ними, т.е. считает их равноценными. На базе отношения слабого предпочтения вводится отношение безразличия (равноценности): два набора x и y безразличны для потребителя, если одновременно выполняются условия «x= 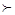y» и «y= 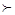x». Факт равноценности двух наборов обычно записывается при помощи«y ~ x». Понятие строгого (сильного) предпочтения 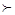определяется следующим образом: «x 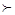y» тогда и только тогда, когда «x= 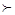y», а соотношение «y= 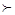x» не имеет места.

В теории потребления обычно исходят из того, что отношение слабого предпочтения удовлетворяет важным предположениям, которые называются аксиомами теории потребления. Таким образом, основой служит использование следующих аксиом:

· Транзитивности: если первая величина сравнима со второй, а вторая – с третьей, то первая сравнима с третьей;

· Полной или совершенной упорядоченности. Согласно ей, потребитель способен упорядочить всевозможные товары или их наборы с помощью отношений предпочтения и безразличия;

· Ненасыщения: если к любому набору товаров добавить дополнительную единицу товара, то полученный набор всегда предпочтительнее прежнего, так как обладает большей полезностью.

Первая аксиома гласит, что рассматриваемое отношение является совершенным, транзитивным и рефлексивным. Совершенность отношения означает для любых двух наборов из множества X обязательно имеет место либо соотношение «x = 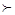y», либо «y = 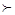x», либо оба вместе, т.е. «x ~ y».

Это означает, что не существует таких наборов, которые потребитель не мог бы сравнить с другими. Транзитивность отношения состоит в том, что из соотношений «x = 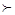y» и «y = 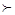z», следует, что «x = 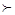z», где x, y, z – потребительские наборы. Это требование отражает совместимость (непротиворечивость) оценок потребителей и вызывает обычно много дополнительных обсуждений. Рефлексивность отношения, т.е. выполнение для любого набора соотношения «x = 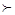x», вытекает из его совершенства.

Следует заметить, что вследствие выполнения первой аксиомы соответствующее отношение безразличия ~ оказывается т.н. отношением эквивалентности. Это означает, что все множество X потребительских наборов распадается на попарно непересекающиеся множества – классы эквивалентности, каждый из которых называется множеством безразличия.

Рассмотрим два примера отношений предпочтения и соответствующих множеств безразличия.

1) Пусть n = 2 и количества продуктов в наборе x=(x₁, x₂) выражены в весовых единицах (кг), а потребитель строит свою сравнительную оценку следующим образом: «набор x предпочтительнее набора y или равноценен ему, если его суммарный вес больше или равен весу второго набора», т.е. «x = 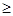y»; если x₁+x₂ = 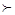y₁+y₂.

Нетрудно видеть, что это отношение удовлетворяет первой аксиоме, и каждый класс безразличия будет состоять из наборов одинакового веса.

2) лексикографическое предпочтение: количества продуктов в наборе x=(x₁, x₂) выражены в любых единицах, потребитель считает первый продукт чрезвычайно ценным и сравнивает наборы по правилу «набор x предпочтительнее набора y, если количество первого продукта в этом наборе больше его количества в наборе y, а если количества первого продукта в обеих наборах равны, то предпочтение определяется по количеству второго продукта».

Этот способ сравнительной оценки определяется формулой:

«x 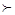y», если x₁ >y₁

или, если x₁ = y₁ и x₂ >y_2.

Это отношение также удовлетворяет первой аксиоме, и каждый набор образует свой собственный класс безразличия.

Для множества безразличия, состоящего из наборов, которые равноценны некоторому набору x, используется обозначение:

C_x = { y Î X ½ y ~ x }.

Обозначим множество всех слабо предпочтительных по отношению к x наборов через 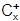, а множество всех слабо не предпочитаемых наборов через .

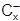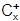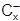Вторая аксиома теории потребления состоит в том, что для любого набора x оба множества и являются замкнутыми подмножествами векторного пространства R_n. Это означает, что оба множества содержат все свои предельные точки и множество безразличия:

,

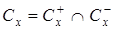т.е. определяется как пересечение этих множеств. Отношение предпочтения, обладающее таким свойством, называется непрерывным.

Из выполнения этих двух основных аксиом вытекает, что существует непрерывная скалярная функция u(x), определенная на связном множестве Xпотребительских наборов и являющаяся индикатором предпочтения, поскольку она обладает следующим характеристическим свойством:

«x = 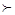y»тогда и только тогда, когда u(x) 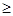u(y).

Таким образом, если потребитель слабо предпочитает набор x набору y, то значение функции uв точке x будет иметь не меньшее значение, чем в точке y, и наоборот, если значение индикатора для некоторого набора x не меньше, чем для набора y, то потребитель слабо предпочитает набор x набору y.

Индикатор предпочтения функции – функцияu(x) –обычно называется функцией полезности потребительских наборов. Нетрудно видеть, что любое монотонное преобразование функции полезности, например функци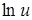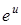и , или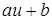(где a>0), опять являются функциями полезности, поскольку они обладают указанным характеристическим свойством. Таким образом, функция полезности не является измерителем какой-то конкретной «полезности», но лишь дает представление о ранжировании (порядке) различных наборов, почему она и называется часто функцией порядковой или ординальной полезности.

Заметим, что каждому множеству С_x безразличия соответствует свое постоянное значение функции полезности : u(x) = const.

Рассмотрим с точки зрения построения функций полезности приведенные выше примеры:

1) «весовое» предпочтение удовлетворяет обеим аксиомам теории потребления, а в качестве функции полезности можно использовать сам вес набора, т.е.

u(x) = u(x₁,x₂) = x₁+x₂;

2) лексиграфическое упорядочение не является непрерывным, поскольку предпочтительное множество (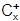 ) и непредпочтительное множество ( 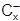)не пересекаются между собой. В связи с этим функция полезности (индикатор предпочтения) здесь не существует.

Порядковый подход к анализу полезности является наиболее распространенным. От потребителя не требуется, чтобы он умел соизмерять блага в каких-то искусственных единицах измерения. Достаточно, чтобы потребитель был способен упорядочить все возможные товарные наборы по их «предпочтительности». В порядковой теории полезности понятие «полезность» означает не что иное, как порядок предпочтения. Утверждение: «Набор А предпочтительнее для данного потребителя, чем набор В», – тоже самое, что и утверждение: «Набор А полезнее для данного потребителя, чем набор В». Вопрос на сколько единиц полезнее набор А, чем набор В не ставится. Потребитель выбирает предпочтительный набор товаров из всех доступных для него.